Welche Arten von gleitenden Durchschnitte gibt es und wie können sie im Trading eingesetzt werden? Ein kurzer Überblick über die wichtigsten gleitenden Durchschnitte und ihre Anwendungsmöglichkeiten.
Inhalt
Was ist ein gleitender Durchschnitt ?
Welche Arten von gleitenden Durchschnitten gibt es ?
Einfacher gleitender Durchschnitt (SMA)
Gewichteter gleitender Durchschnitt (WMA)
Exponentiell gleitender Durchschnitt (EMA)
Kaufman Adaptive Moving Average (KAMA)
Double Exponential Moving Average (DEMA)
Triple Exponential Moving Average (TEMA)
Einsatz von gleitenden Durchschnitten im Trading
Was ist ein gleitender Durchschnitt ?
In der technischen Analyse von Börsenkursen wird ein gleitender Durchschnitt aus den Kursen der Vorperioden berechnet. In einem Tageschart einer Aktie wird der gleitende Durchschnitt zum Beispiel berechnet, indem aus den Schlusskursen der vergangenen Tage ein Durchschnittswert gebildet wird. Für jeden Tag im Chart wird ein neuer Wert berechnet und oberhalb des entsprechenden Tages in den Chart eingetragen. Werden diese Werte nun miteinander verbunden, entsteht die Durchschnittslinie.
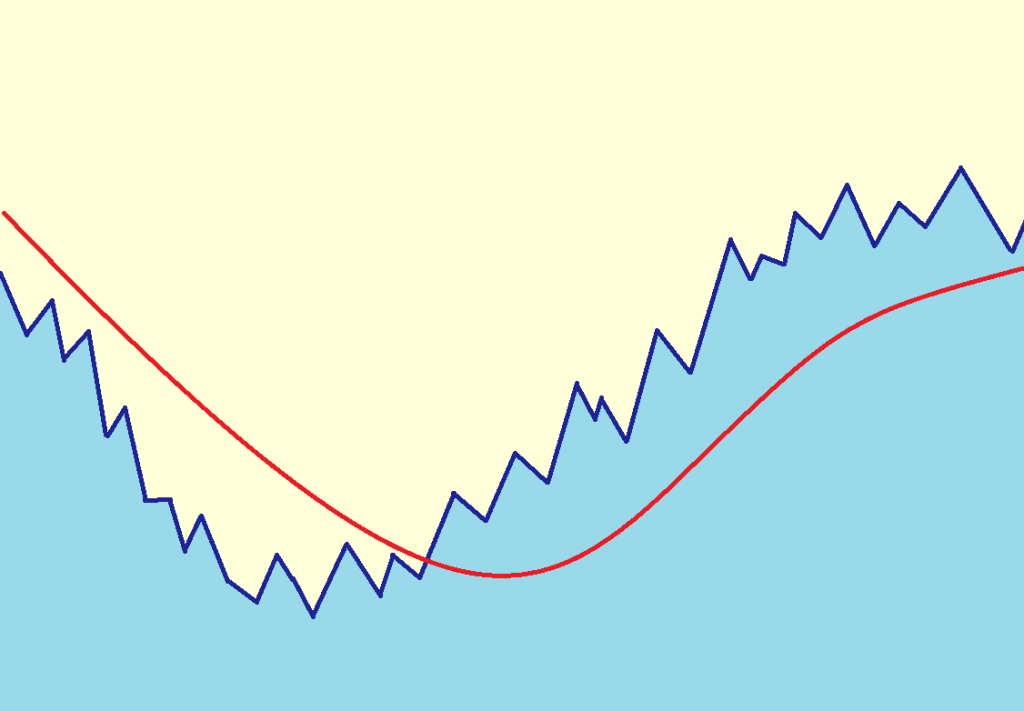
In dem nebenstehenden Chart sehen Sie den Kursverlauf einer Aktie (blau) und einen aus dem Kurs berechneten gleitenden Durchschnitt (rot).
Die Kurslinie zeigt die für Wertpapiere typischen Auf- und Abwärtsbewegungen. Im Gegensatz dazu ist der Verlauf der Durchschnittslinie deutlich glatter. Die kurzfristigen Schwankungen werden also durch den Durchschnitt herausgefiltert und der langfristige Trend ist besser zu erkennen.
Welche Arten von gleitenden Durchschnitten gibt es ?
Zur Berechnung von gleitenden Durchschnitten gibt es eine Vielzahl von Verfahren. Jedes Verfahren berechnet den gleitenden Durchschnitt auf eine andere Art und Weise. Daraus resultierend haben die verschiedenen Durchschnitte andere Werte und die Linien dieser Durchschnitte haben einen unterschiedlichen Verlauf. Jeder Durchschnitt reagiert etwas anders auf Kursänderungen des betrachteten Wertpapiers, weswegen die einzelnen Durchschnitte auch zu unterschiedlichen Zeitpunkten Handelssignale liefern können.
Im Folgenden finden Sie eine Liste mit einigen häufig in der technischen Analyse verwendeten gleitenden Durchschnitten.
Einfacher gleitender Durchschnitt (SMA)
Der einfache gleitende Durchschnitt ist das arithmetische Mittel der letzten x-Zeiteinheiten. Soll beispielsweise der einfache gleitende Durchschnitt der letzten 10 Tage berechnet werden, so werden zuerst die Schlusskurse der letzten 10 Tage zusammengerechnet. Dann wird diese Summe durch die Anzahl der Tage geteilt.
Mehr Informationen zum einfachen gleitenden Durchschnitt
Gewichteter gleitender Durchschnitt (WMA)
Der gewichtete gleitende Durchschnitt wird ähnlich berechnet wie der einfache gleitende Durchschnitt. Allerdings haben beim gewichteten gleitenden Durchschnitt die späteren Kurse einen stärkeren Einfluss auf die Berechnung des Durchschnitts als die früheren Kurse. Hierzu werden die einzelnen Kurse mit einem Faktor multipliziert. Je näher ein Kurs am aktuellen Kurs liegt, desto größer ist der zu multiplizierende Faktor. Der gewichtete gleitende Durchschnitt verläuft normalerweise enger am aktuellen Kurs als der einfache geleitende Durchschnitt.
Mehr Informationen zum gewichteten gleitenden Durchschnitt
Hull gleitender Durchschnitt (HMA)
Zur Berechnung des Hull Moving Average werden zwei gewichtete gleitende Durchschnitte mit unterschiedlicher Periodenlänge verwendet. Diese werden gemäß einer speziellen Formel zusammengerechnet. Danach wird aus den so erzeugten Werten ein neuer gewichteter gleitender Durchschnitt errechnet. Der Hull Moving Average reagiert deutlich schneller auf Trendänderungen als der gewichtete gleitende Durchschnitt. Anders als bei anderen Durchschnitten werden beim Hull Moving Average Trendänderungen der Durchschnittslinie direkt zum Erzeugen von Ein- und Ausstiegssignalen genutzt.
Mehr Informationen zum Hull Moving Average
Triangular Moving Average
Der Triangular Moving Average (TMA) oder dreieckig gleitende Durchschnitt ist ein doppelt geglätteter gleitender Durchschnitt. Um den Triangular Moving Average zu berechnen, wird zuerst ein einfacher gleitender Durchschnitt (SMA) gebildet. Danach wird aus den Werten dieses einfachen gleitenden Durchschnitts ein neuer einfacher gleitender Durchschnitt errechnet.
Mehr Informationen zum Triangular Moving Average
Exponentiell gleitender Durchschnitt (EMA)
Der exponentiell gleitende Durchschnitt wird aus dem aktuellen Kurs und dem exponentiellen Durchschnitt der Vorperiode gebildet. Wie bei den vorherigen Durchschnitten kann auch beim EMA die Periodenlänge eingestellt werden. Allerdings entscheidet hier die Periodenlänge nicht darüber, wie viele Werte in die Berechnung des Durchschnitts mit einbezogen werden. Vielmehr beeinflusst die Periodenlänge hier die Größe des Smoothing Factors (SF) und damit wie groß der Anteil des aktuellen Kurses am neu berechneten Durchschnitt ist. Je größer die Periodenlänge, desto kleiner der SF und desto kleiner der Anteil des aktuellen Kurses am neuen Durchschnitt.
Der exponentiell geglättete Durchschnitt ist neben dem SMA der am meisten im Trading verwendete Durchschnitt.
Mehr Informationen zum exponentiell gleitenden Durchschnitt
Kaufman Adaptive Moving Average (KAMA)
Im Unterschied zu den anderen hier aufgelisteten gleitenden Durchschnitten kann sich der KAMA selbstständig an wechselnde Trendphasen anpassen. Wenn sich der Kurs in einem starken Trend befindet, so steigt auch der KAMA stark an. Geht der Kurs hingegen in eine Seitwärtsbewegung über, wird auch der KAMA automatisch abgebremst. Dadurch verläuft die Durchschnittslinie in Seitwärtsbewegungen oft in einem gewissen Abstand vom Kurs, sodass es seltener zu zufälligem Kreuzen von Kurs und Durchschnittslinie kommt.
Mehr Informationen zum adaptiven gleitenden Durchschnitt.
Double Exponential Moving Average (DEMA)
Der Double Exponential Moving Average wurde entwickelt, um die Verzögerung, mit der gleitende Durchschnitte normalerweise auf einen Trendwechsel im zugrundeliegenden Kurs reagieren, zu verkürzen. Zur Berechnung des DEMA werden ein exponentiell gleitender Durchschnitt und ein aus den ersten exponentiellen Durchschnitt berechneter zweiter Durchschnitt benötigt. Der DEMA verläuft deutlich näher am Kurs als der EMA derselben Periodenlänge.
Mehr Informationen zum Double Exponential Moving Average
Triple Exponential Moving Average (TEMA)
Ebenso wie der DEMA soll auch der TEMA die Verzögerung, mit der gleitende Durchschnitte auf Trendumschwünge reagieren, minimieren. Der TEMA wird aus insgesamt drei verschiedenen exponentiell gleitenden Durchschnitten gebildet. Die Durchschnittslinie des TEMA verläuft noch etwas enger an der Kurslinie als die Linie des DEMA.
Mehr Informationen zum Triple Exponetial Moving Average
Einsatz von gleitenden Durchschnitten im Trading
Gleitende Durchschnitte werden sowohl zum Bestimmen des Trends als auch zum Generieren von Ein- und Ausstiegssignalen genutzt.
Trendbestimmung
Der Trend kann auf zwei Arten bestimmt werden.
- Die Durchschnittslinie wird direkt zum Bestimmen des Trends benutzt. In diesem Fall liegt ein Trendwechsel dann vor, wenn sich die Linie des Durchschnitts in die Gegenrichtung dreht.
- Ein Trendwechsel liegt vor, wenn die Durchschnittslinie die Kurslinie kreuzt. Ein Aufwärtstrend liegt vor, wenn die Durchschnittslinie unterhalb des Kurses verläuft. Ein Abwärtstrend liegt vor, wenn die Durchschnittslinie oberhalb der Kurslinie verläuft.
Einstiegs- und Ausstiegssignale
Signale zum Eröffnen und Schließen einer Position werden erzeugt, wenn sich zwei Linien kreuzen. Auch hier gibt es verschiedene Methoden:
1.) Kreuzen von Kurs und Durchschnitt
Eine Position wird eröffnet, wenn die Durchschnittslinie die Kurslinie kreuzt. Schneidet die Kurslinie die Durchschnittslinie von unten nach oben, so liegt ein Kaufsignal vor. Schneidet die Kurslinie die Durchschnittslinie von oben nach unten, liegt ein Verkaufssignal vor.
2.) Double Crossover Methode
Eine Position wird eröffnet, wenn sich zwei Durchschnittslinien kreuzen. Meistens werden zwei Durchschnittslinien mit unterschiedlichen Periodenlängen verwendet. Schneidet die Durchschnittslinie mit der kürzeren Periodenlänge die Linie mit der längeren Periodenlänge von unten nach oben, so liegt ein Kaufsignal vor. Schneidet sie die Linie mit der längeren Periodenlänge von oben nach unten, so liegt ein Verkaufssignal vor.
Mehr Informationen unter Double Crossover Methode
3.) Triple Crossover Methode
Die Position wird ebenfalls nach dem Kreuzen von zwei Durchschnittslinien eröffnet. Allerdings wird nun eine dritte Durchschnittslinie als Filter verwendet. Nur wenn sich die dritte Durchschnittslinie unterhalb der beiden kreuzenden Linien befindet, darf ein Kaufsignal gehandelt werden. Ebenso darf ein Verkaufssignal nur gehandelt werden, wenn gleichzeitig der dritte Durchschnitt oberhalb der kreuzenden Linien verläuft.
Mehr Informationen unter Triple Crossover Methode
Weitere Artikel
Übersicht | Technische Indikatoren
Moving Average Crossovers | Strategien mit gleitenden Durchschnitten