Der Triangular Moving Average (TMA) oder dreieckig gleitende Durchschnitt ist ein doppelt geglätteter gleitender Durchschnitt. Um den Triangular Moving Average zu berechnen, wird zuerst ein einfacher gleitender Durchschnitt (SMA) gebildet. Danach wird aus den Werten dieses einfachen gleitenden Durchschnitts ein neuer einfacher gleitender Durchschnitt errechnet. Der Triangular Moving Average ist also der einfache gleitende Durchschnitt eines einfachen gleitenden Durchschnitts.
Zwei verschiedene Durchschnitte mit demselben Namen
Irritierenderweise verwenden Broker und Chartprogramme, die den Triangular Moving Average als technischen Indikator in ihrer Software anbieten, zwei verschiedene Varianten des Triangular Moving Average. Diese beiden Varianten werden unterschiedlich berechnet und kommen daher auch zu unterschiedlichen Ergebnissen. Leider geben die meisten Chartprogramme nicht an, welche der beiden Varianten verwendet wurde, sodass der Trader im Zweifel selbst durch Testen herausfinden muss, welche der beiden Varianten im spezifischen Fall vorliegt.
Berechnung des einfachen gleitenden Durchschnitts
Beiden Varianten ist gemeinsam, dass sie einen einfachen gleitenden Durchschnitt oder Simple Moving Average (SMA) für die Berechnung des Durchschnitts benötigen.
Der SMA wird berechnet, indem die Summe der Kurswerte einer bestimmten Periode durch die Periodenlänge geteilt werden. Soll beispielsweise für einen Tageschart der einfache gleitende Durchschnitt mit einer Periodenlänge von 10 berechnet werden, so werden hierfür die Schlusskurse der letzten 10 Tage zusammengerechnet und dann durch die Anzahl der Tage (10) geteilt.
Wenn Sie mehr über den einfachen gleitenden Durchschnitt erfahren möchten, klicken Sie hier.
Für die Berechnung des Triangular Moving Average (TMA) wird in beiden Varianten ein einfacher gleitender Durchschnitt verwendet, der die halbe Periodenlänge des TMA hat. Soll also in einem Tageschart der TMA mit der Periodenlänge 10 berechnet werden, so wird zuerst ein SMA mit der Periodenlänge 5 berechnet. Hat der Triangular Moving Average eine ungerade Periodenlänge, so wird für die Periodenlänge des SMA die nächsthöhere ganze Zahl gewählt. Bei einer Periodenlänge des TMA von 11 wird also der SMA mit einer Periodenlänge von 6 gewählt.
Der SMA wird jeweils für den aktuellen Tag und für die letzen Tage, die dem aktuellen Tag vorangegangen sind, berechnet. Aus diesen SMA-Werten wird nun ein neuer einfacher gleitender Durchschnitt gebildet. Das Ergebnis dieser Berechnung ist der Triangular Moving Average.
Die beiden verschiedenen Varianten des Triangular Moving Average unterscheiden sich lediglich darin, wie viele dieser SMA- Werte zur Berechnung genutzt werden.
Erste Variante
Triangular Moving Average (TMA) mit gerader Periodenlänge
Die Anzahl der zur Berechnung herangezogenen SMA- Werte entspricht der Periodenlänge des verwendeten SMA.
Beispiel:
Bei einem TMA mit der Periodenlänge 4 beträgt die Periodenlänge des SMA 2. Daraus resultierend werden die letzten beiden SMA -Werte zur Berechnung herangezogen.
Bei einem Tageschart sähe die Formel für den TMA wie folgt aus:

Triangular Moving Average mit ungerader Periodenlänge
Ist die Periodenlänge des TMA eine ungerade Zahl, wird die Periodenlänge auf die nächsthöhere Zahl aufgerundet.
Soll beispielsweise der Triangular Moving Average mit einer Periodenlänge von 5 berechnet werden, sieht die Formel wie folgt aus:
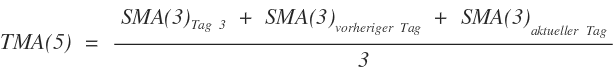
Zweite Variante
Triangular Moving Average mit ungerader Periodenlänge
Die Berechnung des TMA, wenn die Periodenlänge eine ungerade Zahl ist, ist identisch mit der Berechnung in Variante 1.
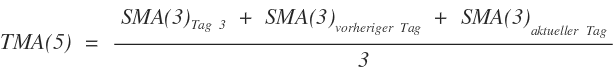
Triangular Moving Average mit gerader Periodenlänge
Bei der Berechnung eines TMA mit gerader Periodenlänge wird hingegen etwas anders vorgegangen.
Um zu ermitteln, wie viele SMA- Werte zur Berechnung genutzt werden müssen, wird zur Periodenlänge des SMA die Zahl 1 hinzuaddiert. Bei einem TMA mit einer Periodenlänge von 4 wird beispielsweise der SMA mit einer Periodenlänge von 2 genutzt. Im Unterschied zur ersten Variante, werden nun aber die ersten 3 SMA- Werte (2 + 1) verwendet. Die so erzeugte Summe wird nun ebenfalls durch die Zahl drei geteilt.
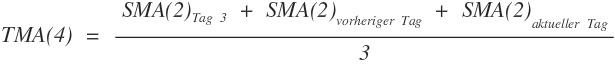
Die mit Hilfe der beiden verschiedenen Varianten erzeugten TMA- Werte weichen in der Regel nicht sonderlich voneinander ab. Besonders bei großen Periodenlängen dürfte die Abweichung in den meisten Fällen zu vernachlässigen sein. Bei kleineren Periodenlängen kann es aber durchaus vorkommen, dass bei der einen Variante ein Trading Signal ausgelöst wird und bei der anderen nicht.
Der Triangular Moving Average im Vergleich zum einfachen gleitenden Durchschnitt
Da der Triangular Moving Average aus den Werten eines einfachen gleitenden Durchschnitts gebildet wird, reagiert er auf Kursveränderungen langsamer als der einfache gleitende Durchschnitt selbst. In der Regel wechselt der TMA die Trendrichtung, nachdem der SMA die Richtung geändert hat.
Grundsätzlich kann der Triangular Moving Average, wie alle anderen Durchschnitte auch, zum Erzeugen von Tradingsignalen genutzt werden.
Zwei häufig genutzte Tradingsysteme, die gleitende Durchschnitte nutzen sind die Double Moving AverageCrossover Methode, die zwei kreuzende gleitende Durchschnitte nutzt, und die Triple Moving Average Crossover Methode, die drei gleitende Durchschnitte nutzt.
Verwandte Artikel
Übersicht | Die bekanntesten gleitenden Durchschnitte im Überblick
Gewichteter gleitender Durchschnitt
Was ist der Hull Moving Average?