Der exponentiell gleitende Durchschnitt ist ein technischer Indikator, der sowohl zur Trendbestimmung, als auch zum Erzeugen von Handelssignalen genutzt werden kann. Ein exponentiell gleitender Durchschnitt (EMA) wird mit Hilfe des exponentiell gleitenden Durchschnitts der Vorperiode und des aktuellen Kurses berechnet. Anders als bei anderen Durchschnitten braucht man für die Berechnung des exponentiell gleitenden Durchschnitts also nur zwei Werte.
Neben dem einfachen gleitenden Durchschnitt ist der exponentiell gleitende Durchschnitt der am häufigsten in der technischen Analyse eingesetzte Durchschnitt.
Im Englischen wird der exponentiell gleitende Durchschnitt als Exponential Moving Average (EMA) bezeichnet.
Inhalt
Was ist der exponentiell gleitende Durchschnitt?
Berechnung des exponentiell gleitenden Durchschnitts
Berechnung des EMA anhand eines Beispiels
Vergleich exponentiell gleitender Durchschnitt und einfacher gleitender Durchschnitt
Einsatz des exponentiell gleitenden Durchschnitts im Trading
Was ist der exponentiell gleitende Durchschnitt?
Der exponentielle gleitende Durchschnitt wird zur Analyse von Börsenkursen verwendet. Wie alle gleitenden Durchschnitte wird der exponentiell gleitende Durchschnitt als Linie direkt in den Kurschart eingezeichnet. Soll der Durchschnitt beispielsweise in einen Tageschart eingetragen werden, wird dafür zuerst für jeden Tag der gleitende Durchschnitt nach der im unten folgenden Abschnitt vorgestellten Formel berechnet. Dann werden die Werte der einzelnen Durchschnitte oberhalb der einzelnen Tage in den Chart eingetragen und zur Durchschnittslinie verbunden.
Berechnung des exponentiell gleitenden Durchschnitts
Zur Berechnung des exponentiellen Durchschnitts werden der aktuelle Kurs, der exponentiell gleitende Durchschnitt der Vorperiode und der sogenannte Smoothing Factor benötigt. Die Größe des Smoothing Factors ist von der gewählten Periodenlänge abhängig.
Formel
Für die Berechnung des exponentiell gleitenden Durchschnitts (EMA) gibt es verwirrenderweise zwei Formeln.
Formel 1 EMAt = Ct * SF + (1-SF) *EMAt-1
Formel 2 EMAt = (Ct – EMAt-1) * SF + EMAt-1
Die beiden Formeln können aber ineinander überführt werden. Daraus resultierend müssen die beiden Formeln auch zum selben Ergebnis kommen.
Schauen wir uns die erste Formel einmal genauer an:
EMAt = Ct * SF + (1-SF) *EMAt-1
mit:
- EMAt = exponentiell gleitender Durchschnitt der betrachteten Periode (bspw. des heutigen Tages)
- EMAt-1 = exponentiell gleitender Durchschnitt der vorherigen Periode (bspw. des gestrigen Tages)
- Ct = Endkurs der betrachteten Periode (bspw. Schlusskurs des heutigen Tages)
- SF = Smoothing Factor
Was ist der Smoothing Factor?
Der Smoothing Factor hat immer einen Wert zwischen 0 und 1 und gibt an, welchen Anteil der heutige Kurs an der Berechnung des heutigen exponentiellen Durchschnitts hat.
Bei einem SF von 0,1 setzt sich der neue EMA zum Beispiel zu 10 Prozent aus dem Tagesendkurs und zu 90 Prozent aus dem vorherigen EMA zusammen. Umgekehrt besteht der neue exponentiell gleitende Durchschnitt bei einem Smoothing Factor von 0,9 zu 90 Prozent aus dem aktuellen Schlusskurs und zu 10 Prozent aus dem vorherigen Durchschnitt.
Je größer der SF, desto größer ist der Anteil des aktuellen Kurses am neu berechneten EMA und desto näher ist der Durchschnitt am aktuellen Kurswert.
Wie wird der Smoothing Factor berechnet?
Die Formel für den Smoothing Factor lautet:
SF = 2/ (n+1)
Wobei n die Anzahl der Perioden ist.
Bei einem 10 Tage EMA beträgt die Periodenlänge 10. Daraus resultierend lautet die Formel für den SF:
SF = 2/(10+1) = 2/11 = 0,18
Bei einem 20 Tage EMA wäre der SF
2/(20+1) = 0,09
Je länger also die Periodenlänge, desto kleiner ist der Smoothing Factor und desto geringer der Anteil des aktuellen Kurses am EMA. Daraus resultierend verläuft ein EMA mit einer kurzen Periodenlänge näher am Kurs als ein EMA mit langer Periodenlänge.
Berechnung des EMA anhand eines Beispiels
Zur Verdeutlichung berechnen wir im Beispiel unten den exponentiell gleitenden Durchschnitt für die letzten 5 Kerzen. Berechnet werden soll der 5 Tage EMA.

Zuerst berechnen wir den Smoothing Factor. Die Periodenlänge ist 5. Eingesetzt in die Formel bedeutet das:
2/(5+1) = 2/6 = 0,33
Für den ersten Tag können wir die Formel zur Berechnung des EMA nicht benutzen, da wir den EMA der Vorperiode nicht kennen. Deshalb wird zur Berechnung des ersten EMA einfach der Schlusskurs des Vortags an Stelle des EMAt-1 eingesetzt. Die Formel lautet also
EMAt = Ct * SF + (1-SF) *Ct-1
Die Tagesendkurse der einzelnen Tage können Sie in der obigen Graphik in den gelben Kästchen auf der linken Seite ablesen. Der Schlusskurs der fünftletzten Kerze beträgt 104. Der Kurs ihrer Vorkerze betrug 105,5. Eingesetzt in die Formel bedeutet das:
104 * 0,33 * (1-0,33)*105,5 = 105,005
Für die folgenden Werte können wir die normale Formel verwenden.
EMAt = Ct * SF + (1-SF) *EMAt-1
Der Endkurs der viertletzten Kerze ist 103,5. Der EMA der Vorkerze beträgt, wie oben berechnet, 105,005.
103,5 * 0,33+ (1-0,33) * 105,005 = 104,508
Für jede der nun folgenden Kerzen wird nun nach obigem Verfahren der exponentielle Durchschnitt errechnet.
Trägt man die Durchschnitte der aufeinanderfolgenden Tage in einen Chart ein, so erhält man eine Punktlinie. Verbindet man die einzelnen Punkte, so erhält man die exponentiell geglättete Durchschnittslinie, die zur technischen Analyse eingesetzt wird.
Exponentiell gleitender Durchschnitt und einfacher gleitender Durchschnitt im Vergleich.
Der exponentiell gleitende Durchschnitt und der einfache gleitende Durchschnitt (Simple Moving Average SMA) sind die beiden mit Abstand am häufigsten benutzten gleitenden Durchschnitte.
Der einfache gleitende Durchschnitt wird gebildet, indem das arithmetische Mittel der letzten x Kerzen gebildet wird. Zur Ermittlung des einfachen gleitenden Durchschnitts der letzten 10 Tage werden also die Schlusskurse der letzten 10 Tage zusammengezählt und dann durch die Anzahl der Tage geteilt.
Hier haben wir auch schon den ersten Unterschied zwischen den beiden Durchschnitten. Der SMA betrachtet ausschließlich die Kerzen, die innerhalb des gewählten Betrachtungszeitraums liegen. Der 10 Tage SMA berechnet sich zum Beispiel nur aus Kerzen innerhalb der letzten 10 Tage. Die elfte Kerze hat keinerlei Einfluss mehr auf die Berechnung des Durchschnitts. Da sich der Berechnungszeitraum jeden Tag um einen Tag verschiebt, sind im Endeffekt nur zwei Kerzen für die Wertänderung des neuen Durchschnitts verantwortlich: Die aktuelle Kerze, die neu hinzukommt, und die letzte Kerze, die aus dem neuen Berechnungszeitraum herausfällt.
Gerade bei sehr kurzen Periodenlängen kann das zu plötzlichen Sprüngen der Durchschnittlinie führen.
Als Beispiel betrachten wir den Chart unten, für den die 5 Tage SMA Linie gebildet werden soll. Durch den gelben Kasten sind die jeweils fünf letzten Kerzen gekennzeichnet, aus denen der gleitende Durchschnitt berechnet wird.
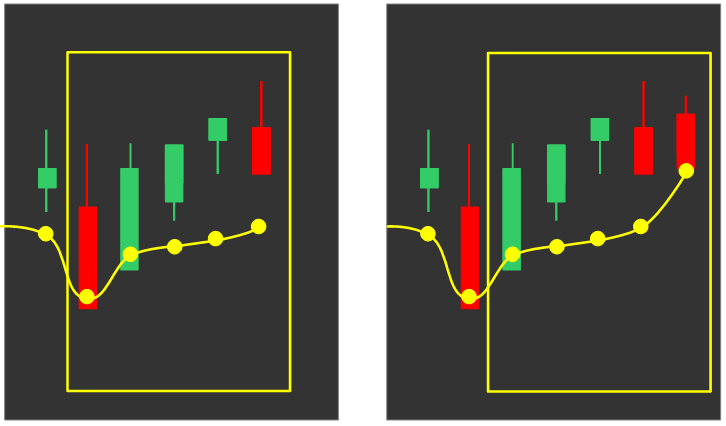
Auf der linken Seite liegen die Schlusskurse der fünf Kerzen alle recht nah beieinander. Die einzige Ausnahme ist der zweite Tag, an dem es zu einem scharfen Einbruch nach unten gekommen ist. Der Ausbruch wurde am Folgetag direkt wieder durch eine Gegenbewegung kompensiert. Dennoch sorgt dieser Tag für einen deutlich tieferen Durchschnittswert.
Im Bild auf der rechten Seite ist eine neue Kerze hinzugekommen. Da die lange Ausbruchskerze nun die sechste Kerze ist, fällt sie aus dem Berechnungszeitraum heraus. Dadurch springt der SMA plötzlich nach oben, obwohl sich der aktuelle Kurs fast gar nicht bewegt hat.
Beim EMA besteht dieses Problem nicht. Hier hat die Periodenlänge nur indirekt über den Smoothing Factor Einfluss auf die Berechnung des Durchschnitts.
Unterschiedliche Gewichtung der Vortage
Ein weiterer Unterschied ist die Gewichtung der einzelnen Tage. Im SMA hat jeder Tag den gleichen Einfluss auf den Durchschnitt. Im EMA hingegen hat nur der letzte Tag einen direkten Einfluss auf die Berechnung des neuen Durchschnitts.
Die anderen Tage haben allerdings einen indirekten Einfluss auf die Berechnung des neuen EMA, da sie in die Berechnung des EMA des Vortages mit eingeflossen sind. Bei der Berechnung EMA des Vortages wiederum hatte der Schlusskurs des Vortages einen besonders großen Einfluss. Daraus folgend haben also die Kurse der letzten Tage einen größeren Einfluss auf den Durchschnitt als die früheren Tage.
Der EMA befindet sich daher meistens näher am aktuellen Kurs als der SMA. Daraus folgend verläuft auch die Durchschnittslinie des EMA enger am Kurs und löst deshalb früher ein Durchbruchssignal aus.
Einsatz des exponentiell gleitenden Durchschnitts im Trading
Wie die meisten gleitenden Durchschnitte lässt sich der exponentiell gleitende Durchschnitt sowohl zur Bestimmung des Trends, als auch zum Erzeugen von Handelssignalen nutzen.
Bestimmung des Trends
Gleitende Durchschnitte werden häufig dazu verwendet, um festzustellen, ob sich der Kurs aktuell in einem Aufwärtstrend, einem Abwärtstrend oder einem Seitwärtstrend befindet. Um mit Hilfe des exponentiell gleitenden Durchschnitts den Trend zu bestimmen, gibt es verschiedene Möglichkeiten.
Zum einen kann die Richtung des gleitenden Durchschnitts selbst Aufschluss über den Trend geben.
- Steigt der gleitende Durchschnitt, befindet sich der Kurs in einem Aufwärtstrend.
- Fällt die Linie des Durchschnitts befindet sich der Kurs in einem Abwärtstrend.
- Verläuft die Linie des gleitenden Durchschnitts seitlich oder unter leichten Schwankungen, so befindet sich der Kurs in einem Seitwärtstrend.
Häufig überprüfen Trader auch, auf welcher Seite des gleitenden Durchschnitts sich der Kurs befindet. Verläuft der Kurs oberhalb der Linie des gleitenden Durchschnitts, befindet er sich in einem Aufwärtstrend. Notiert der Kurs hingegen unterhalb des gleitenden Durchschnitts, liegt ein Abwärtstrend vor.
Erzeugen von Handelssignalen
Der exponentiell gleitende Durchschnitt kann auch direkt dazu genutzt werden, um Handelssignale zum Einstieg und Ausstieg zu generieren. Handelssignale können dabei auf verschieden Arten erzeugt werden:
- Bei der einfachsten Methode wird immer dann ein Signal zum Kauf oder Verkauf erzeugt, wenn der Kurs die Linie des gleitenden Durchschnitts kreuzt. Ein Kaufsignal liegt immer dann vor, wenn der Kurs über die Durchschnittslinie steigt. Verkauft wird immer, wenn der Kurs unter die Linie des Durchschnitts fällt.
- Bei der Double Crossover Methode werden zwei verschiedene Durchschnitte beobachtet. Hier wird immer dann ein neues Signal erzeugt, wenn sich die beiden Durchschnitte kreuzen.
- Die Triple Crossover Methode verwendet drei verschiedene gleitende Durchschnitte. Bei dieser Strategie wird immer dann eine neue Position eröffnet, wenn die drei Durchschnitte in der richtigen Reihenfolge übereinanderliegen.
Der EMA als Bestandteil anderer technischer Indikatoren
Der exponentiell gleitende Durchschnitt ist nicht nur selbst ein sehr beliebter Indikator, sondern er dient auch als Grundlage für eine ganze Reihe weiterer Indikatoren. Der DEMA und der TEMA sind beides gleitende Durchschnitte, zu deren Berechnung nicht nur ein exponentiell gleitender Durchschnitt benötigt wird, sondern die zusätzlich weitere exponentielle Durchschnitte verwenden, die aus den Werten des ersten exponentiellen Durchschnitts berechnet wurden. Sowohl der DEMA als auch der TEMA reagieren schneller auf Kursänderungen als der EMA.
Auch Indikatoren, die keine gleitenden Durchschnitte sind, nutzen den exponentiell gleitenden Durchschnitt. Bei Trendkanälen wie Envelopes oder dem Keltner Channel wird die Linie des EMA beispielsweise als Mittellinie des Kanals genutzt. Ebenso verwendet der bekannte MACD Indikator die Linien von zwei exponentiell gleitenden Durchschnitten zur Erzeugung von Signalen.
Bücher zum Thema Technische Analyse
Technische Analyse der Finanzmärkte
von John J. Murphy
Einer der Klassiker unter den Börsenbüchern.
Das Buch gibt einen Einblick in die verschiedenen Bereiche der technischen Analyse. Die behandelten Themen reichen dabei von Chartformationen über Elliot Wellen bis hin zu Börsenzyklen.
Technische Indikatoren – simplified
von Oliver Paesler
Ein kurzer Überblick über die wichtigsten Technischen Indikatoren
Weitere Artikel
Liste der bekanntesten gleitenden Durchschnitte
Moving Average Crossovers | Trading Strategien mit gleitenden Durchschnitten
10 Trendfolge Strategien kurz vorgestellt