Der Kaufman Adaptive Moving Average oder adaptive gleitende Durchschnitt unterscheidet sich von anderen gleitenden Durchschnitten dadurch, dass er selbstständig erkennt, ob sich der betrachtete Kurs in einer Trendphase oder in einer Seitwärtsbewegung befindet. In Trendphasen bewegt sich die Durchschnittslinie dieses Indikators überdurchschnittlich schnell. In Seitwärtsphasen oder bei Trendwechseln hingegen wird die Durchschnittslinie automatisch abgebremst.
Inhalt
Was ist der Kaufman Adaptive Moving Average?
Berechnung des Kaufman Adaptive Moving Average
Erklärung der Funktionsweise anhand eines Beispiels
Vergleich adaptiver gleitender Durchschnitt mit anderen gleitenden Durchschnitten.
Verwendung des Kaufman Adaptive Moving Average in der technischen Analyse
Was ist der Kaufman Adaptive Moving Average?
Der Kaufman Adaptive Moving Average wurde von Perry J. Kaufman entwickelt. Häufig wird die Abkürzung KAMA für den Durchschnitt verwendet.
Das Besondere am KAMA ist, dass bei der Berechnung des gleitenden Durchschnitts die Stärke der Kursbewegung gemessen wird. Bewegt sich der Kurs über einen längeren Zeitraum in eine Richtung, kommt es beim KAMA zu einem starken Anstieg oder Fall der Durchschnittlinie. Endet die Trendbewegung, flacht die Linie des KAMA deutlich ab.
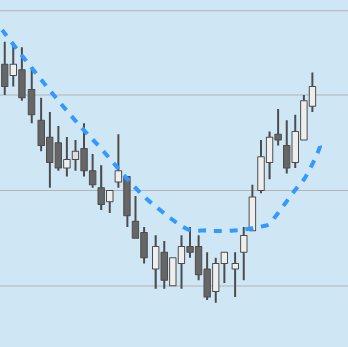
Der Chart zeigt die Linie des Kaufman Adaptive Moving Average in einem Kerzenchart.
Auf der linken Seite des Charts befindet sich der Kurs in einer starken Abwärtsbewegung. In diesem Bereich des Charts bewegt sich auch die Linie des KAMA (blau) steil nach unten.
Dann kommt es zu einem Trendumschwung. Der KAMA beendet hier seine Abwärtsbewegung und geht in eine Seitwärtsbewegung über.
Charakteristisch für den KAMA ist der sehr flache Verlauf der Durchschnittslinie während eines Trendumschwungs.
Berechnung des Kaufman Adaptive Moving Average
Die Formel zur Berechnung des adaptiven gleitenden Durchschnitt erinnert an die Formel des exponentiellen gleitenden Durchschnitts. Zur Berechnung des aktuellen Durchschnitts werden der Wert des Durchschnitts der Vorperiode und der aktuelle Kurs benötigt.
Formel
KAMAt = αt *(Ct – KAMAt-1) + KAMAt-1
mit
KAMAt = Zu berechnender adaptiver gleitender Durchschnitt
KAMAt-1 = Adaptiver gleitender Durchschnitt der Vorperiode
Ct = aktueller Kurs
αt = Der Wert von αt muss zuerst mit Hilfe der unten stehenden Formel berechnet werden
Formel αt
αt = [ERt * (SCfast -SCslow) + SCslow]2
Zur Berechnung von α werden drei Werte benötigt:
ERt = die Efficiency Ratio
SCfast = die schnelle Glättungskonstante (fast Smoothing Constant)
SCslow = die langsame Glättungskonstante (slow Smoothing Constant)
Schauen wir uns diese drei Werte etwas genauer an.
Berechnung der Efficiency Ratio
Das Herzstück des Kaufman Adaptive Moving Average ist die Efficiency Ratio. Mit Hilfe der Efficiency Ratio (ER ) soll festgestellt werden, ob sich der Kurs in einem Trend oder einer trendlosen Phase befindet. Hierzu werden zwei Werte berechnet, die Nettokursbewegung und die Bruttokursbewegung.
Nettokursbewegung
Die Nettokursbewegung misst die Handelsspanne des Kurses vom ersten Tag der Beobachtungsperiode bis zum letzten Tag der Beobachtungsperiode. Um einen 10 Tage Durchschnitt zu berechnen, werden also die Kurse der letzten 10 Tage betrachtet. Zur Berechnung der Nettokursbewegung wird der erste Kurs des ersten Tages vom Schlusskurs des letzten Tage abgezogen.
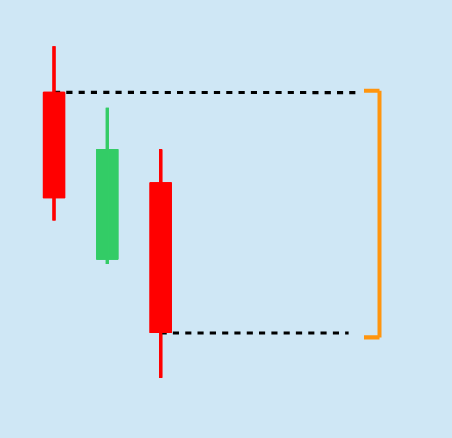
In dem nebenstehenden Bild soll die Nettokursbewegung für die drei abgebildeten Kerzen berechnet werden. Hierzu wird der Anfangskurs der ersten Kerze vom Schlusskurs der letzten Kerze abgezogen. Die Nettokursbewegung wird in dem Bild durch die orange Spanne angezeigt.
Die Spanne zwischen den Kursen wird immer als positiver Wert angegeben. Auch wenn der Schlusskurs, wie in diesem Beispiel, unterhalb des Anfangskurses liegt, hat die Handelsspanne, und damit die Nettokursbewegung, einen positiven Wert.
Bruttokursbewegung
Die Bruttokursbewegung misst die Gesamtsumme der Handelsspannen der einzelnen Tage.
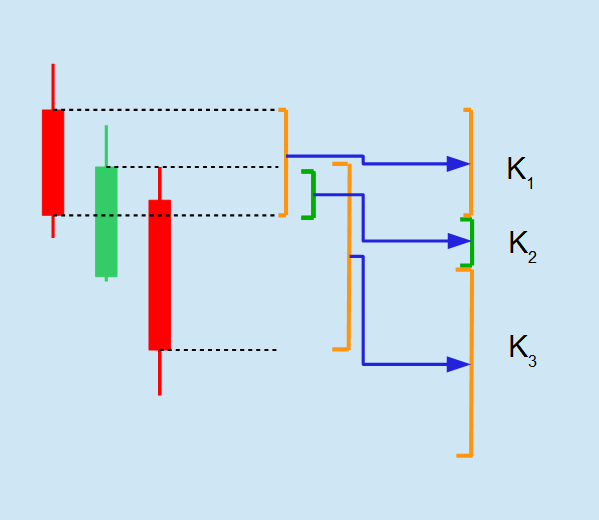
Für jeden einzelnen Tag wird die Spanne zwischen dem Schlusskurs des betrachteten Tages und dem Schlusskurs des Vortages berechnet. Anschließend werden die so ermittelten Handelsspannen zusammengezählt.
In dem Bild links sehen Sie wieder die drei Kerzen von oben. Nun soll die Bruttokursbewegung der drei Kerzen berechnet werden. Hierzu wird zuerst die Handelsspanne jeder einzelnen Kerze getrennt berechnet (K1, K2, K3). Dann wird die Bruttokursbewegung errechnet, indem die drei Handelsspannen zusammengerechnet werden.
Zu Ermittlung der Efficiency Ratio (ER) wird nun der Wert der Nettokursbewegung (NKB) durch den Wert der Bruttokursbewegung (BKB) geteilt.
ER = NKB / BKB
Da die Bruttokursbewegung immer größer oder gleich der Nettopreisbewegung sein muss, bewegt sich der Wert der ER immer zwischen 0 und 1.
Efficiency Ratio in Trendphasen und in Seitwärtsbewegungen
Als Nächstes wollen wir untersuchen, wie sich die Efficiency Ratio in Trendphasen und Seitwärtsbewegungen verhält.
Wenn der Kurs während einer starken Trendbewegung an jedem einzelnen Tag steigt, dann entspricht die Nettokursbewegung der Bruttokursbewegung und die Efficiency Ratio hat den Wert 1.
In einer Seitwärtsbewegung befindet sich der Schlusskurs des letzten Tages sehr nah am Anfangskurs des ersten Tages, die Nettokursbewegung ist daher also relativ klein. Da es zumeist innerhalb des Seitwärtstrends Schwankungen gibt, ist die Bruttokursbewegung dennoch relativ hoch. Dadurch hat die ER in einer Seitwärtsbewegung einen kleinen Wert.
In Trendphasen hat die Efficiency Ratio einen Wert nahe 1, in Seitwärtsphasen und bei Trendwechseln hat die Efficiency Ratio einen Wert nahe 0.
Berechnung der Glättungskonstanten
Kommen wir nun wieder zurück zur Berechnung des α. Für die Berechnung werden neben der Efficiency Ratio zwei Glättungskonstanten (Smoothing Constants SC) benötigt.
Die Formeln für die beiden Glättungskonstanten sehen Sie unten.
schnelle Glättungskonstante SCfast = 2/(x+1)
langsame Glättungskonstante SCslow = 2/(y+1)
Die Werte für x und y können sie in ihrem Chartprogramm unter Minimalwert (x) und Maximalwert (y) einstellen.
Für den Minimalwert wird eine relativ kleine Zahl ausgewählt. Kaufmann hat hier den Wert 2 empfohlen.
Für den Maximalwert wird eine größere Zahl eingesetzt. Hier hat Kaufmann einen Wert von 30 empfohlen.
Eingesetzt in die Formeln für die Glättungskonstanten heißt das:
schnelle Glättungskonstante SCfast = 2/(x+1) = 2/(2+1) = 2/3 = 0,666
langsame Glättungskonstante SCslow = 2/(y+1) = 2/(30+1) = 2/31 = 0,0645
Der Wert der schnellen Glättungskonstante ist also deutlich größer als der Wert der langsamen Glättungskonstante.
Berechnung von αt
Da wir nun alle zur Berechnung nötigen Faktoren kennen, wenden wir uns wieder der Formel für αt zu.
αt = [ERt * (SCfast -SCslow) + SCslow]2
Die Formel kann umgeschrieben werden in.
αt = [ERt *SCfast + (1-ERt ) * SCslow]2
Die untere Formel zeigt, dass bei einer Efficiency Ratio nahe 1 fast nur der SCfast in die Berechnung des αt einfließt. Ist die Efficiency Ratio dagegen relativ klein, so fließt vermehrt der SCslow in die Berechnung mit ein.
Setzen wir nun die Glättungskonstanten von oben ein.
αt = [ERt *0,666 + (1-ERt ) *0,0645]2
Je größer der ER Wert, desto größer ist also der Wert für α. Bei einer kleinen Efficiency Ratio, ist auch der Wert für α kleiner.
Berechnung des adaptiven gleitenden Durchschnitt
Nachdem wir α kennen, können wir nun den adaptiven gleitenden Durchschnitt berechnen.
KAMAt = αt *(Ct – KAMAt-1) + KAMAt-1
Auch diese Formel kann in eine andere Formel überführt werden
KAMAt = αt *Ct + (1- αt) * KAMAt-1
Wenn Sie die obige Formel betrachten, sehen Sie, dass der Wert des αt darüber entscheidet, welchen Anteil der aktuelle Kurs Ct und der vorherige Durchschnitt KAMAt-1 am neu berechneten Durchschnitt haben.
- Je größer αt , desto größer ist der Anteil des aktuellen Kurses am neuen Durchschnitt.
- Je kleiner αt , desto größer ist der Anteil des vorherigen Durchschnitts am neuen Durchschnitt.
Da die Größe von αt vom Trend abhängt, kann auch gesagt werden:
- Je ausgeprägter der Trend, desto größer der Einfluss des aktuellen Kurses auf die Berechnung des neue Durchschnitts und desto stärker steigt oder fällt der Durchschnitt.
- Je schwächer der Trend, desto größer der Anteil des vorherigen Durchschnitts und desto kleiner ist die Veränderung des Durchschnitts.
Erklärung der Funktionsweise anhand eines Beispiels
Um die Funktionsweise des Kaufman Adaptive Moving Average besser zu verstehen, betrachten wir den fiktiven Kursverlauf einer Aktie. Wir nehmen an, dass die Aktie zuerst 10 Tage unverändert bei 100€ notiert. Dann steigt der Kurs der Aktie für 10 Tage um jeweils genau einen Euro. Im Anschluss daran fällt die Aktie jeden Tag um exakt einen Euro pro Tag.
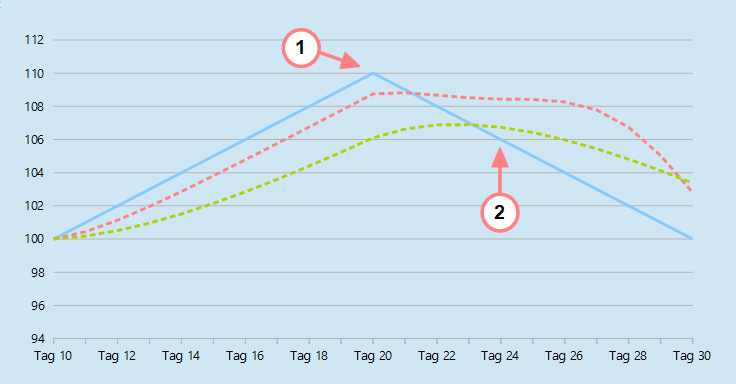
Im Chart oben ist der Kursverlauf der Aktie in Blau eingezeichnet. Die ersten 10 Tage werden nicht gezeigt, da der Kurs sich hier nicht bewegt. Der Verlauf des 10 Tage KAMA ist durch die rote Linie dargestellt. Zum Vergleich ist zusätzlich der exponentiell gleitende Durchschnitt als grüne Linie eingezeichnet.
Wir betrachten nun zwei Punkte im Chart, für die wir den 10 Tage KAMA berechnen wollen. Die Punkte sind durch die beiden Pfeile markiert.
Punkt 1
Bei Punkt 1 ist der Kurs die letzten 10 Tage um je 1€ gestiegen. Der Kurs befindet sich an diesem Punkt also in einer Aufwärtsbewegung.
Punkt 2
Bei Punkt 2 hat der Kurs sein Hoch bereits vor 4 Tagen überschritten. Der Kurs ist also in den vergangenen 10 Tagen zuerst für 6 Tage gestiegen und ist dann für 4 Tage gefallen.
Schritt 1 | Berechnung der Efficiency Ratio
Zuerst müssen wir die Efficiency Ratio berechnen. Da wir den KAMA 10 berechnen, betrachten wir die Kurse der letzten 10 Tage.
Punkt 1
Der Kurs ist in den letzten 10 Tagen jeden Tag um einen Euro gestiegen. Der Gesamtanstieg oder die Nettokursbewegung beträgt also 10€. Beim Bruttokursanstieg werden die täglichen Kursbewegungen zusammengerechnet. Der Kurs bewegt sich 10 mal um je einen Euro. Der Bruttokursanstieg liegt damit also ebenfalls bei 10€.
Die Efficiency Ratio beträgt also 10/10 = 1
Punkt 2
Bei Punkt 2 gab es erst einen Anstieg um 6€ und dann eine Abwärtsbewegung um 4€. Am Ende der 10 Tage steht der Kurs also 2 Euro über dem Anfangskurs. Die Nettokursbewegung liegt daher bei 2€. Da die Kurse sich jeden Tag um 1€ bewegt haben, liegt die Bruttokursbewegung wie zuvor bei 10€.
Der Wert der Efficiency Ratio liegt damit bei 2/10 = 0,2.
Schritt 2 | Berechnung von α
Wir können nun die ER Werte der beiden Punkte in die Formel für α einsetzen.
αt = [ERt * (SCfast -SCslow) + SCslow]2
Die Formel kann umgeschrieben werden zu:
αt = [ERt *SCfast + (1-ERt ) * SCslow]2
Zur Berechnung der Glättungskonstanten nutzen wir die von Kaufman vorgeschlagenen Standarteinstellungen von 2(min) und 30(max). Damit haben die beiden Glättungskonstanten die folgenden Werte:
schnelle Glättungskonstante SCfast = 2/(x+1) = 2/(2+1) = 2/3 = 0,666
langsame Glättungskonstante SCslow = 2/(y+1) = 2/(30+1) = 2/31 = 0,0645
Wir setzen die beiden Werte in die Formel für α ein.
αt = [ERt *SCfast + (1-ERt ) * Scslow]2
αt = [ERt *0,666 + (1-ERt ) *0,0645]2
Punkt 1
Bei Punkt 1 hat die Efficiency Ratio einen Wert von 1.
α10 = [1*0,666 + (0) *0,0645]2
α10 = 0,443556
Wenn der Wert der Efficiency Ratio ein großer Wert ist, erhalten wir auch einen großen Wert für α.
Punkt 2
Der ER Wert bei Punkt 2 ist hingegen mit 0,2 deutlich kleiner.
α10 = [0,2*0,666 + (0,8) *0,0645]2
α10 = 0,03415104
Bei einem kleinen ER Wert ist der Anteil der langsamen Glättungskonstant SCslow deutlich größer. Daraus resultierend ist der Wert für α kleiner als bei einem hohen ER Wert.
Schritt 3 | Berechnung des Kaufman Adaptive Moving Average
Nachdem wir die Werte für α berechnet haben, können wir sie nun in die Formel für den Kaufman Adaptive Moving Average einfügen.
KAMAt = αt *Ct + (1- αt) * KAMAt-1
Punkt 1
Der aktuelle Kurs liegt bei 110€ .
Der Wert des vorherigen KAMA betrug 107,7519093.
KAMA(10) = 0,443556 *110 + (1-0,443556) * 107,7519093
Der aktuelle KAMA beträgt also 108,7490634
Bei Punkt 1 ist der Wert für α sehr hoch( de facto ist es der höchstmögliche Wert für α). Daraus resultierend hat der neue Kurs einen großen Anteil am neuen KAMA. Im Vergleich zum vorherigen KAMA notiert der neue KAMA dadurch deutlich höher, sodass die Durchschnittslinie steigt.
Bei einem großen Wert für α hat der Kurs also einen relativ großen Anteil am neuen KAMA, während der alte KAMA einen relativ kleinen Anteil hat. Der KAMA bewegt sich dadurch stark in Richtung des Kurses.
Punkt 2
Bei Punkt 2 liegt der aktuelle Kurs bei 106€. Der Wert des vorherigen KAMA lag bei 108,51882
KAMA(10) = 0,03415104 *106 + (1-0,03415104) * 108,52882
aktueller KAMA 108,4327996
Beim zweiten Punkt ist der Wert für α deutlich kleiner. Der alte KAMA hat an diesem Punkt also einen großen Anteil am Wert des neuen KAMA. Dadurch bewegt sich die Linie des KAMA an dieser Stelle seitlich.
Ist der Wert von α relativ klein, so hat der alte KAMA einen deutlich größeren Anteil an der Berechnung des neuen KAMA. Die beiden Werte liegen dadurch näher beieinander, was dazu führt dass die Linie des gleitende Durchschnitts flacher verläuft.
Vergleich des adaptiven gleitenden Durchschnitts mit anderen gleitenden Durchschnitten.
Im Vergleich zu anderen gleitenden Durchschnitten reagiert der adaptive gleitende Durchschnitt sehr viel schneller auf Trendwechsel.
Charakteristisch für den adaptiven Durchschnitt ist, dass er am Ende einer Trendbewegung sehr schnell in eine flache Seitwärtsbewegung übergeht. Dies geschieht, da bei einer Seitwärtsbewegung des Kurses das α sehr klein wird, und somit der vorherige Durchschnitt mit dem neuen Durchschnitt beinahe identisch ist.
In den meisten Fällen bewegt sich die Linie des KAMA dabei in einiger Entfernung zum Kurs, sodass es nicht zu einem ständigen Kreuzen zwischen Kurs und Durchschnittslinie kommt, wie das oft bei anderen Durchschnitten der Fall ist.
Verwendung des Kaufman Adaptive Moving Average in der technischen Analyse
Wie die meisten gleitenden Durchschnitte wird auch der adaptive gleitende Durchschnitt sowohl zum Ermitteln des vorherrschenden Trends als auch zum Erzeugen von Ein- und Ausstiegssignalen genutzt.
Trendbestimmung
Zur Bestimmung des Trends gibt es zwei Möglichkeiten:
Bei der erste Methode zeigt der Verlauf der Durchschnittslinie den Trend an. Steigt die Linie des KAMA über einen längeren Zeitraum, liegt ein Aufwärtstrend vor. Einen Abwärtstrend erkennt man daran, dass die Linie des KAMA fällt. Verläuft die Linie des KAMA relativ flach befinden wir uns entweder in einem Seitwärtstrend oder es bahnt sich ein Trendwechsel an.
Bei der zweiten Methode wird die Position des Kurses im Verhältnis zur Linie des Durchschnitts betrachtet. Verläuft der Kurs oberhalb der Linie des KAMA, liegt ein Aufwärtstrend vor. Verläuft der Kurs unterhalb der Linie, liegt ein Abwärtstrend vor. In Phasen ohne klaren Trend kommt es häufig zu einem Kreuzen der Durchschnittslinie mit dem Kurs. Hier hat der Kaufman Adaptive Moving Average einen Vorteil gegenüber anderen Durchschnitten, da die Linie des Durchschnitts in diesen Phasen häufig oberhalb der Kurslinie verläuft und es dadurch zu weniger Kreuzungen und dadurch auch zu weniger Fehlsignalen kommt.
Erzeugen von Trading Signalen
Auch hier gibt es mehrere Möglichkeiten:
Eine neue Position kann eröffnet werden, wenn der Kurs die Durchschnittslinie kreuzt. Steigt der Kurs über die Linie des Kaufman Adaptive Moving Average, entsteht ein Kaufsignal. Fällt der Kurs unter den KAMA, erhalten wir ein Verkaufssignal.
Bei der Double Crossover Methode werden Signale zum Einstieg und Ausstieg erzeugt, wenn sich die Linien von zwei Durchschnitten kreuzen.
Bei der Triple Crossover Methode werden drei gleitende Durchschnitte verwendet, die in der richtigen Reihenfolge angeordnet sein müssen, damit ein Signal entsteht.
Weitere Artikel
Liste der bekanntesten gleitende Durchschnitte
Moving Average Crossovers | Strategien mit gleitenden Durchschnitten
10 Trendfolgestrategien kurz vorgestellt