SMA, EMA und WMA sind drei gleitende Durchschnitte, die in der technischen Analyse von Börsenkursen eingesetzt werden. Die Linien der drei Durchschnitte werden in den Kurschart eingetragen und können so zur Bestimmung des Trends und zum Erzeugen von Trading Signalen verwendet werden.
Der Exponential Moving Average (EMA), der Simple Moving Average (SMA) und der Weighted Moving Average (WMA) sind die drei am häufigsten in der technischen Analyse eingesetzten gleitenden Durchschnitte.
Inhalt
Was sind EMA, SMA und WMA?
Unterschiedliche Berechnung von SMA, EMA und WMA
Berechnung des SMA
Berechnung des EMA
Berechnung des WMA
Vergleich der unterschiedlichen Berechnungsmethoden
Unterschiede in der Reaktionen auf Kursänderungen
Was sind EMA, SMA und WMA?
EMA, SMA und WMA sind drei gleitende Durchschnitte, die nach unterschiedlichen Verfahren aus den Schlusskursen von Aktien, Indizes oder Rohstoffen berechnet werden.
Beim SMA und beim WMA wird dabei aus einer bestimmten Anzahl von Schlusskursen ein Mittelwert berechnet. Zur Berechnung des EMA reichen hingegen lediglich der aktuelle Schlusskurs und der vorherige EMA.
Aufgrund der Tatsache, dass die Durchschnitte auf verschiedene Art und Weise berechnet werden, haben die Linien der drei Durchschnitte einen unterschiedlichen Verlauf. Werden die Linien der Durchschnitte zum Trading eingesetzt, kommt es daher häufig zu unterschiedlichen Zeitpunkten zu Trading Signalen.
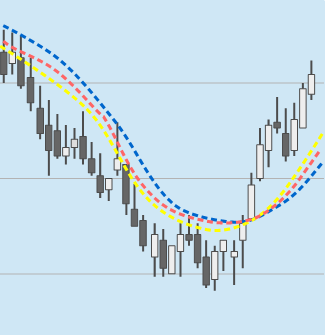
Im nebenstehenden Kerzenchart markieren die drei farbigen Linien den Verlauf der drei gleitenden Durchschnitte.
Auch wenn sich die drei Linien grundsätzlich in die gleiche Richtung bewegen, hat doch jede der drei Durchschnittslinien ihren eigenen Verlauf.
Auf Deutsch werden die drei Durchschnitte auch als exponentiell gleitender Durchschnitt (EMA), als einfacher gleitender Durchschnitt (SMA) und als gewichteter gleitender Durchschnitt (WMA) bezeichnet.
Unterschiedliche Berechnung von SMA, EMA und WMA
Um die Unterschiede zwischen den drei Durchschnitten besser zu verstehen, werfen wir zuerst einen Blick auf die Berechnung der Durchschnitte.
Berechnung des SMA
Zur Berechnung des SMA wird zuerst eine bestimmte Anzahl an Schlusskursen zusammengerechnet und dann durch die Anzahl der Schlusskurse geteilt. Bei einem SMA der letzten 10 Tage (SMA 10) wir der Durchschnitt zum Beispiel aus den Schlusskursen der letzten 10 Tage berechnet. Hierzu werden zuerst die Schlusskurse der letzten 10 Tage zusammengerechnet. Im zweiten Schritt wird die so errechnete Summe durch die Anzahl der Tage geteilt.
Die allgemeine Formel für den SMA sieht wie folgt aus:
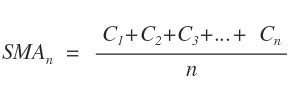
mit
Ct = Kurs
n = Periodenlänge
Beispiel
Schauen wir uns dazu die Berechnung anhand eines Beispiels an. Wir möchten den SMA 5, den 5 Tage Durchschnitt, für den Kurs einer Aktie berechnen. Dazu sehen wir uns zuerst die letzten 5 Schlusskurse an.
Tag1 | 98,00€
Tag 2 | 101,50€
Tag 3 | 102,00 €
Tag 4 | 100,50€
Tag 5| 101,00€
Um den Durchschnitt zu berechnen, müssen wir zuerst die Summe der fünf Schlusskurse bilden.
98,00€ + 101,50€ + 102,00€ + 100,50€ + 101,00 €
= 503€
Nun wird das Ergebnis durch die Anzahl der Tage geteilt.
503€ / 5 = 100,60 €
Der Wert des Simple Moving Average für den letzten Tag beträgt also 100,60€.
Mehr Informationen zum SMA finden Sie im Artikel zum einfachen gleitenden Durchschnitt (SMA).
Berechnung des WMA
Der WMA wird im Grunde sehr ähnlich berechnet wie der SMA. Auch hier werden die Schlusskurse der letzten Tage zusammengerechnet. Allerdings werden hier die Schlusskurse vorher mit einem Gewichtungsfaktor multipliziert. Dieser Gewichtungsfaktor ist umso höher, je näher der Tag am aktuellen Tag liegt. Wenn ein 10 Tage Durchschnitt berechnet wird, erhält der erste Tag der Berechnung einen Gewichtungsfaktor von 1 und der letzte Tag einen Gewichtungsfaktor von 10. Nachdem die so errechneten Werte zusammengerechnet wurden, werden sie durch die Summe der Gewichtungsfaktoren geteilt, um so den gleitenden gewichteten Durchschnitt oder WMA zu erhalten.
Beispiel
Das oben beschriebene Vorgehen hört sich in der Theorie komplizierter an, als es in der Praxis wirklich ist. Schauen wir uns dazu wieder unser Beispiel von oben an. Die Schlusskurse der 5 Tage sind diesmal auf der linken Seite der Tabelle zu finden.
| Schlusskurs | Gewichtungsfaktor | Schlusskurs*GF | |
| Tag 1 | 98,00€ | 1 | 98,00€*1 |
| Tag 2 | 101,50€ | 2 | 101,50€*2 |
| Tag 3 | 102,00€ | 3 | 102,00€*3 |
| Tag 4 | 100,50€ | 4 | 100,50€*4 |
| Tag 5 | 101,00€ | 5 | 101,00€*5 |
| Summe | 15 | 1514,00€ |
Im ersten Schritt werden den einzelnen Schlusskursen die zugehörigen Gewichtungsfaktoren zugewiesen. Der erste Tag ist am weitesten vom aktuellen Tag entfernt und erhält daher den Gewichtungsfaktor 1. Der letzte Tag erhält den Gewichtungsfaktor 5. In der rechten Spalte werden die einzelnen Kurse mit den zugehörigen Gewichtungsfaktoren multipliziert. Werden die fünf so errechneten Werte im Anschluss zusammengerechnet, erhält man eine Summe von 1514 (Spalte 4). Als Zweites werden die Gewichtungsfaktoren zusammengerechnet. In diesem Fall erhalten wir eine Summe von 15 (Spalte 3). Zuletzt wird das Ergebnis von Spalte 4 durch das Ergebnis von Spalte 3 geteilt und wir erhalten den gewichteten gleitenden Durchschnitt oder WMA.
In unserem Fall hat der WMA einen Wert von 100,933.
Mehr zum WMA finden Sie im Artikel zum gewichteten gleitenden Durchschnitt.
Berechnung des EMA
Die Berechnung des EMA unterscheidet sich deutlich von den vorherigen beiden Durchschnitten. Der EMA wird ausschließlich aus dem aktuellen Kurs und dem EMA des Vortages berechnet.
EMAt = Ct * SF + (1-SF) *EMAt-1
mit
EMAt = exponentiell gleitender Durchschnitt der betrachteten Periode (bspw. des heutigen Tages)
EMAt-1 = exponentiell gleitender Durchschnitt der vorherigen Periode (bspw. des gestrigen Tages)
Ct = Kurs
SF = Smoothing Factor
SF = 2/ (n+1)
n = Periodenlänge (Anzahl der Tage)
Wie Sie sehen, hat die Anzahl der Tage beim EMA nur über den Smoothing Factor Einfluss auf die Berechnung des Durchschnitts.
- Wenn eine große Anzahl an Tagen zur Berechnung verwendet wird, hat der Smoothing Factor einen kleinen Wert und der Anteil des aktuellen Kurses am EMA ist ebenfalls relativ klein.
- Bei einer kleinen Anzahl an Tagen ist der Wert des Smoothing Factors größer und dadurch ist auch der Anteil des aktuellen Kurses am EMA größer.
Beispiel
Auch hier wollen wir für die Aktie von oben den 5 Tage Durchschnitt berechnen. Zur Berechnung des EMA brauchen wir diesmal allerdings lediglich den letzten Schlusskurs der Aktie. Zusätzlich benötigen wir den Wert des vorherigen EMA. Wir nehmen an, dass dieser Wert bei 100,50€ lag.
Zuerst berechnen wir den Smoothing Factor. Dazu setzen wir die Anzahl der Tage in die Formel für den Smoothing Faktor ein.
SF = 2/(5+1) = 0,333
Nun haben wir alle Werte, um sie in die Formel von oben einzusetzen.
EMAt = Ct * SF + (1-SF) *EMAt-1
EMA5 = 101,00€*0,333 + (1- 0,333)*100,50€
EMA5 = 100,666
Der Wert des exponentiell gleitenden Durchschnitts liegt also bei 100,666€
Mehr zum EMA finden Sie im Artikel zum exponentiell gleitenden Durchschnitt.
Vergleich der unterschiedlichen Berechnungsmethoden
Bei der Betrachtung der drei Beispiele von oben fällt auf, dass die Werte der drei errechneten Durchschnitte voneinander abweichen. Der SMA hat einen Wert von 100,60€, der WMA hat einen Wert von 100,93€ und der EMA notiert bei 100,66€. Die drei Durchschnitte werden also nicht nur auf unterschiedliche Art berechnet, sondern die Berechnungen kommen auch zu unterschiedlichen Ergebnissen. Dies führt dazu, dass auch die Linien der Durchschnitte einen unterschiedlichen Verlauf haben müssen.
Schauen wir uns nun die Unterschiede in den Berechnungen genauer an.
Unterschied zwischen SMA und WMA
Sowohl der SMA als auch der WMA nutzen eine festgelegte Anzahl an Schlusskursen. In unserem Beispiel wurden zum Beispiel in beiden Fällen die Schlusskurse von 5 Tagen verwendet.
Beim SMA ist der Einfluss jedes Schlusskurses auf den Wert des Durchschnitts genau gleich groß. In unserem Beispiel machte jeder Tag genau ein Fünftel des Durchschnitts aus. Beim WMA hingegen hat jeder Tag aufgrund der Gewichtungsfaktoren einen unterschiedlichen Einfluss auf den Wert des Durchschnitts. In unserem Beispiel ist der Einfluss des letzten Tages beispielsweise fünfmal so hoch wie der Einfluss des ersten Tages. Daraus resultierend verändert sich der Wert des WMA bei einem Kursanstieg am letzten Tag deutlich stärker als der Wert des SMA.
Unterschied zwischen EMA und den anderen beiden Durchschnitten
Im Unterschied zu den anderen beiden Durchschnitten wird zur Berechnung des EMA nur der letzte Kurs benötigt. Auch wenn von einem 5 Tage Durchschnitt gesprochen wird, hat die Anzahl der Tage nur indirekt über den Smoothing Factor einen Einfluss auf die Berechnung.
Auf den ersten Blick haben die Kurse vor dem letzten Tag daher gar keinen Einfluss auf den aktuellen EMA. Tatsächlich haben Sie allerdings über den EMA der Vorperiode doch einen gewissen Einfluss auf die Berechnung , da der vorherige EMA direkt oder indirekt aus den vorherigen Schlusskursen berechnet wurde. Beim EMA 5 beeinflussen daher sogar Schlusskurse, die mehr als 5 Tage zurückliegen, die Berechnung des aktuellen Durchschnitts.
Im Gegensatz dazu werden beim SMA und WMA tatsächlich nur die Schlusskurse einer begrenzten Anzahl von Tagen betrachtet.
Diese Art der Berechnung kann gerade beim SMA unerwartete Konsequenzen haben.
Soll beim SMA am Folgetag ein neuer Durchschnitt berechnet werden, so fällt der letzte Tag des alten Durchschnitts (der jetzt sechste Tag) aus der Berechnung heraus. Gleichzeitig wird der neue Tag neu in die Berechnung hinzugenommen. Die Wertänderung des SMA hängt also von der Differenz zwischen dem sechsten Tag und dem neuen Tag ab. Als Konsequenz daraus kann es passieren, dass die Linie des Durchschnitts stark springt, wenn ein Tag mit einer großen Kursbewegung aus der Berechnung herausfällt, selbst wenn der aktuelle Tag ein relativ ruhiger Tag gewesen ist. Dieses Phänomen tritt vor allem bei Durchschnitten mit einer sehr kleinen Anzahl an Tagen auf. Bei Durchschnitten mit einer größeren Anzahl hingegen ist dieser Effekt weniger ausgeprägt, da ein einzelner Tag hier generell weniger Einfluss auf den Durchschnitt hat.
Beim WMA haben wir im Prinzip denselben Effekt. Allerdings ist dieser Effekt hier nicht so gravierend, da der erste Kurs durch den Gewichtungsfaktor keinen großen Einfluss mehr auf die Berechnung hat.
Beim EMA hingegen kann es aufgrund der andersartigen Berechnung überhaupt nicht zu dieser Art vor Kurssprüngen kommen.
Unterschiede in der Reaktion auf Kursänderungen
Aufgrund der Unterschiede in der Berechnung reagieren SMA, EMA und WMA auch unterschiedlich schnell auf Kursänderungen. Um dies zu demonstrieren, sehen wir uns das unten stehende Beispiel an.
Für unser Beispiel nehmen wir an, dass sich eine Aktie die ersten 10 Tage überhaupt nicht bewegt und konstant bei 100 € notiert. Ab dem elften Tag beginnt die Aktie jeden Tag um genau einen Euro zu steigen.
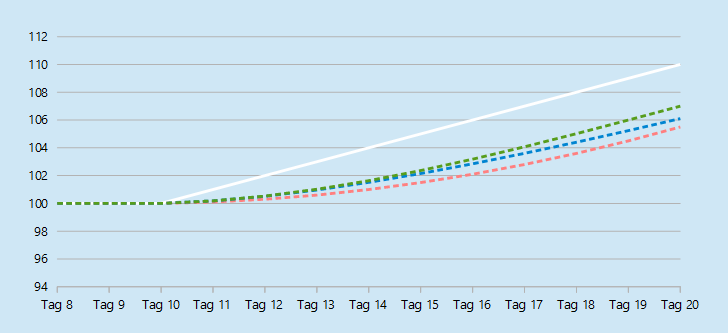
Die weiße Linie in dem oben stehenden Chart zeigt den Kursverlauf der Aktie. Eingezeichnet sind hier nur die Tage acht bis zwanzig.
Für diese Aktie wurden nun sowohl der 10 Tage EMA, der 10 Tage SMA als auch der 10 Tage WMA berechnet. Die rote Linie im Chart zeigt den Verlauf des SMA, die blaue Linie zeigt den EMA und durch die grüne Linie ist der Verlauf des WMA eingezeichnet.
Es ist deutlich zu sehen, dass die drei Durchschnitte mit unterschiedlichen Geschwindigkeiten ansteigen.
Der stärkste Anstieg ist im WMA zu sehen, der gleich zu Beginn stärker anzog und auch im weiteren Verlauf schneller zulegte als die anderen beiden Durchschnitte. Als Zweites folgte der EMA, der in der Mitte der drei Durchschnitte liegt. Den Schluss bildete der SMA der den geringste Anstieg der drei Durchschnitte verzeichnete.
Die drei Durchschnitte im Börsenchart
Ein ähnliches Verhalten können wir auch in realen Börsencharts beobachten.
Der WMA reagiert am stärksten auf Kursänderung und verläuft daher, zumindest in Trendphasen, am engsten am Kurs. Der EMA reagiert etwas weniger sensitiv auf Kursänderungen und verläuft daher etwas weiter vom Kurs entfernt als der WMA. Der SMA ist in Trendphasen am weitesten vom Kurs entfernt. Auffällig ist auch, dass der SMA auf kurzfristige Gegenbewegungen deutlich weniger stark reagiert als die anderen beiden Durchschnitte.
Kommt es zu einem Trendumbruch, drehen WMA und EMA häufig etwas früher als der langsamere SMA. Allerdings sind sie dadurch auch etwas anfälliger für mögliche Fehlsignale.
Viele Trader nutzen ein Kreuzen von Kurs und Durchschnittslinie als Signal zum Ein- und Ausstieg. Dadurch, dass die Linien der drei gleitenden Durchschnitte einen unterschiedlichen Verlauf haben, kommt es auch zu unterschiedlichen Zeitpunkten zu einem Kreuzen mit dem Kurs. Dadurch haben Trading Strategien je nach verwendetem Durchschnitt eine unterschiedliche Performance. Allerdings lässt sich hier nicht klar sagen, welcher Durchschnitt besser ist als der andere. Je nach betrachteter Aktie oder Indizes erzielt mal der eine Durchschnitt und mal der andere Durchschnitt eine bessere Performance.
Weitere Artikel zum Thema gleitende Durchschnitte
Liste | Die bekanntesten gleitenden Durchschnitte
Die 200 Tage Linie und ihr Einsatz im Trading
Moving Average Crossovers | Strategien mit gleitenden Durchschnitten