Der Triple Exponential Moving Average (TEMA) ist ein gleitender Durchschnitt, der besonders schnell auf Kursänderungen und Trendwechsel reagiert. Der TEMA wird aus den Werten von mehreren exponentiell gleitenden Durchschnitten berechnet.
Inhalt
Was ist der Triple Exponential Moving Average?
Berechnung des Triple Exponential Moving Average
Vergleich mit anderen gleitenden Durchschnitten
Trading mit dem Triple Exponential Moving Average
Was ist der Triple Exponential Moving Average?
Der Triple Exponential Moving Average (TEMA) ähnelt in seinem Aufbau sehr dem Double Exponential Moving Average (DEMA) und wurde wie dieser von Patrick Mulloy entwickelt. Bei beiden Durchschnitten war es das Ziel, die Verzögerungszeit, mit der gleitende Durchschnitte normalerweise auf Kursbewegungen reagieren, so weit wie möglich zu reduzieren.
In der technischen Analyse von Börsenkursen wird vor allem die Linie des TEMA verwendet.
Um die Linie des Durchschnitts zu erstellen, wird zuerst für für jeden Tag der Triple Exponentiel Moving Average berechnet. Anschließend werden die Werte in den Kurschart eingetragen und zur Durchschnittslinie verbunden.
In unserem Chart zeigt die rote Line den Verlauf des 10 Tage TEMA. Im Vergleich zu anderen Durchschnitten verläuft der TEMA sehr nah am Kurs.
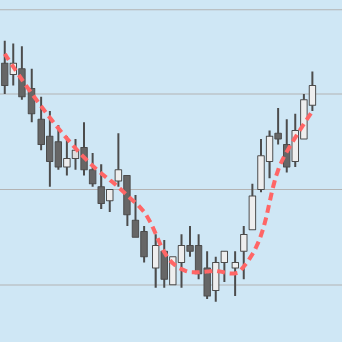
Gerade bei sehr kurzfristigen Durchschnitten, wie der 10 Tage Linie, kommt es daher häufig zu Überschneidungen zwischen Kurs und der Linie des Triple Exponential Moving Average.
Berechnung des Triple Exponential Moving Average
Die Berechnung des Triple Exponenetial Moving Average ist recht aufwändig und erfolgt in mehreren Schritten. Glücklicherweise können die meisten Chartprogramme die Linie des TEMA für Sie berechnen und nehmen Ihnen somit die Berechnung des Durchschnitts ab. Trotzdem lohnt es sich, sich mit der Berechnung des TEMA etwas auseinanderzusetzen, um so die Funktion des Durchschnitts besser zu verstehen.
Schauen wir uns dazu zuerst die Formel des Triple Exponential Moving Average an.
Formel Triple Exponential Moving Average
TEMAt = 3*EMAt– 3*EMA(EMAt) + EMA[EMA(EMAt)]
Zur Berechnung des TEMA werden also drei Werte benötigt, der exponentiell gleitende Durchschnitt EMAt , ein aus den Werten des exponentiellen Durchschnitts berechneter zweiter exponentieller Durchschnitt EMA(EMAt) und ein dritter exponentieller Durchschnitt EMA[EMA(EMAt), der aus den Werten des zweiten Durchschnitts berechnet wurde.
Zur Berechnung des TEMA wird also zuerst der exponentielle gleitende Durchschnitt (EMA) für die gewählte Periodenlänge berechnet. Aus den Werten dieses EMA werden sodann die beiden weiteren exponentiell gleitenden Durchschnitte gebildet. Im letzten Schritt werden dann alle diese Werte in die Formel des TEMA eingesetzt.
Die Berechnung des TEMA erfolgt in vier Schritten.
Schritt 1.
Im ersten Schritt wird der exponentiell gleitende Durchschnitt für eine bestimmte Periodenlänge berechnet. Soll zum Beispiel der 10 Tage TEMA berechnet werden, muss zuerst der 10 Tage EMA berechnet werden.
EMAt = Ct * SF + (1-SF) *EMAt-1
Zur Berechnung des exponentiell gleitenden Durchschnitts werden der aktuelle Kurs C und der vorherige Durchschnitt EMAt-1 benötigt.
Mehr Informationen zur Berechnung des EMA (inklusive Beispiel) finden Sie im Artikel zum exponentiell gleitenden Durchschnitt.
Schritt 2.
Aus den Werten des in Schritt 1 errechneten EMA wird nun ein zweiter EMA berechnet. Dieser EMA ist also der exponentielle gleitende Durchschnitt des ersten EMA.
EMA(EMAt) = EMAt * SF + (1-SF) * EMA(EMAt-1)
Ein Beispiel für die Berechnung des EMA(EMAt) finden Sie im Artikel zum Double Exponential Moving Average.
Schritt 3.
Aus dem in Schritt 2 errechneten EMA wird im Anschluss ein dritter EMA errechnet. Es wird also der exponentielle gleitende Durchschnitt des exponentiellen gleitenden Durchschnitts des exponentiellen gleitenden Durchschnitts berechnet.
EMA[EMA(EMAt)] = EMA(EMAt)*SF + (1-SF)*EMA[EMA(EMAt-1)]
Schritt 4.
Die drei zuvor berechneten gleitenden Durchschnitte werden nun in die Formel des Triple Exponential Moving Average eingesetzt.
TEMAt = 3*EMAt– 3*EMA(EMAt) + EMA[EMA(EMAt)]
Der Triple Exponential Moving Average wird für mehrere aufeinanderfolgende Tage berechnet. Die Werte des TEMA können im Anschluss in einen Chart eingetragen werden. Werden die einzelnen Punkte verbunden, entsteht die Durchschnittslinie des TEMA.
Wie funktioniert der TEMA?
Um zu verstehen, wie sich der Triple Exponential Moving Average bei Kursbewegungen verhält, schauen wir uns zuerst an, wie die drei Bestandteile der Formel, der EMA, der EMA(EMA) und der EMA[EMA(EMA)] auf Kursbewegungen reagieren.
Test | Wie reagieren die einzelnen Bestandteile auf Kursänderungen
Dazu nehmen wir an, das eine Aktie zuerst für 10 Tage konstant bei hundert Euro notiert. Im Anschluss steigt die Aktie für 10 Tage jeden Tag um genau einen Euro. Die letzten 10 Tage fällt die Aktie jeden Tag um einen Euro. Für diese Aktie berechnen wir nun vier 10 Tage Durchschnitte, den TEMA, den EMA, den EMA(EMA) und den EMA[EMA(EMA)] .
Im Chart unten sehen Sie den Verlauf der vier Durchschnitte.
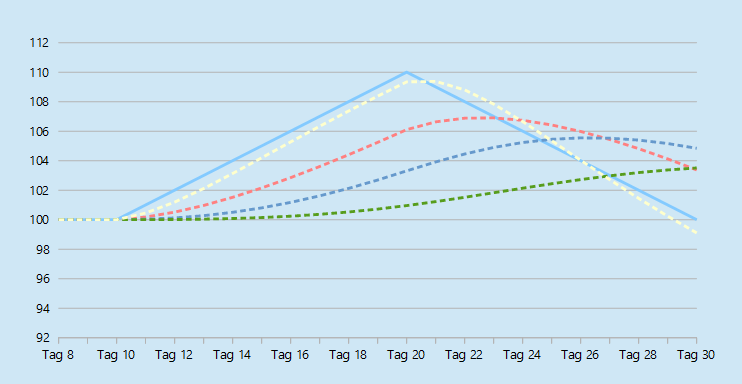
Der Kursverlauf der Aktie wird durch die blaue Linie markiert. Die gelbe Linie ist der TEMA, die rote Linie ist der EMA, die blaue Linie zeigt den EMA(EMA)und die grüne Linie den EMA[EMA(EMA)] .
Der TEMA selbst reagiert deutlich stärker auf Kursbewegungen als die anderen drei Durchschnitte und verläuft daher deutlich näher am Kurs.
Wie beschleunigt und verlangsamt der TEMA?
Wir konzentrieren uns aber zunächst auf den EMA und den EMA(EMA), der auch als doppelt geglätteter EMA bezeichnet wird. Der EMA (rot) reagiert deutlich stärker auf Kursbewegungen als der geglättete EMA (blau) und steigt und fällt daher deutlich stärker.
Schauen wir uns nun noch einmal die Formel des Triple Exponential Moving Average an.
TEMAt = 3*EMAt– 3*EMA(EMAt) + EMA[EMA(EMAt)]
Die Formel kann umgeschrieben werden zu:
TEMAt = EMA[EMA(EMAt)] + [3*EMAt– 3*EMA(EMAt)]
Der Inhalt der eckigen Klammer [3*EMAt– 3*EMA(EMAt)] wird also zum dreifach geglätteten Durchschnitt, dem EMA[EMA(EMAt)], hinzugerechnet. Wenn wir nun noch einmal den Chart betrachten, sehen wir, dass der EMA (rot) bei länger steigenden Kursen über dem geglätteten EMA (blau) verläuft. Der Wert innerhalb der Klammer ist in diesem Fall also positiv und wird daher zum EMA[EMA(EMA)] hinzugerechnet.
Fallen die Kurse hingegen über einen längeren Zeitraum, liegt der EMA über dem EMA(EMA). Dies können Sie auf der rechten Seite des Charts sehen. Der EMA ist in diesem Fall also kleiner als der EMA(EMA) , sodass der Wert innerhalb der Klammer negativ wird und der Wert vom EMA[EMA(EMA)]abgezogen wird.
Je größer der Abstand zwischen den beiden Durchschnitten, desto größer ist der Wert, der von EMA[EMA(EMA)] abgezogen oder aufgeschlagen wird.
Je stärker also die Steigung der Kurse, desto stärker wird der Wert des TEMA beschleunigt oder abgebremst.
Vergleich mit anderen gleitenden Durchschnitten
Als Nächstes wollen wir untersuchen, wie schnell der Triple Exponential Moving Average im Vergleich zu anderen gleitenden Durchschnitten auf Kursbewegungen reagiert. Wir betrachten dazu noch einmal die Aktie aus dem vorherigen Abschnitt.
Nun berechnen wir für diese Aktie erneut den exponentiell gleitenden Durchschnitt (EMA), der einer der am häufigsten in der technischen Analyse verwendeten Durchschnitte ist, und den Double Exponential Moving Average (DEMA). Wie schon am Anfang dieses Artikels erwähnt, wurde der DEMA ebenfalls mit dem Ziel entwickelt, die Reaktionszeit des Durchschnitts zu begrenzen.
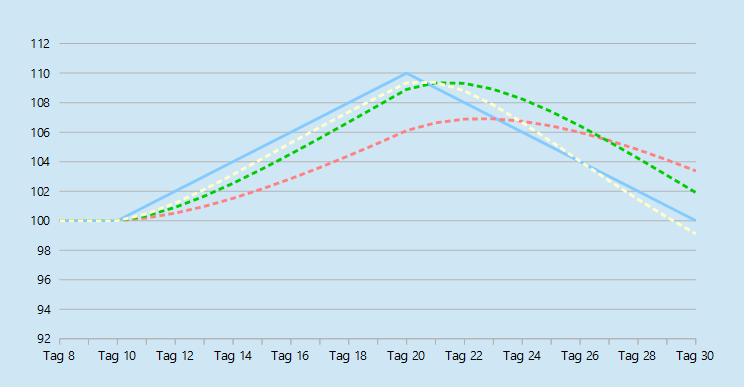
Die gelbe Linie zeigt wieder den Verlauf des TEMA, die rote Linie zeigt den EMA. Durch die grüne Linie wird der Verlauf des DEMA angezeigt.
Wie Sie schon im vorherigen Abschnitt gesehen haben, reagiert der TEMA deutlich schneller auf Kursbewegungen als der EMA. Auch drehte der TEMA nach dem Trendwechsel des Kurses deutlich früher als der EMA.
Auch im Vergleich zum DEMA zeigte der TEMA eine etwas schnellere Reaktionszeit. Auffällig bei den beiden Durchschnitten ist, dass sie beide extrem nah am Kurs verlaufen. Bei Trendwechseln schneidet der Kurs den gleitenden Durchschnitt dadurch extrem früh. Allerdings besteht hier auch die Gefahr, dass der Durchschnitt bei einem kurzen Kursrücksetzer vom Kurs geschnitten wird und es so zu einem falschen Trading Signal kommt.
Trading mit dem Triple Exponential Moving Average
Da der Triple Exponential Moving Average schnell auf Trendwechsel reagiert und nah am Kurs verläuft, ist der TEMA gut dazu geeignet, den Trend zu visualisieren. Dazu wird einfach der Verlauf der Linie des Durchschnitts betrachtet. Bewegt sich die Linie nach oben, liegt ein Aufwärtstrend vor. Fällt die Linie, befindet sich der Kurs in einer Abwärtsbewegung. Bewegt sich die Linie unter leichten Schwankungen seitlich, liegt ein Seitwärtstrend vor.
Der Triple Exponential Moving Average kann auch zum Erzeugen von Trading Signalen eingesetzt werden. Dafür werden meistens mehrere gleitende Durchschnitte gleichzeitig verwendet.
Bei der bekanntesten Variante, dem Double Moving Average Crossover, werden zwei gleitende Durchschnitte genutzt. Zum Beispiel könnten ein 20 Tage Durchschnitt und ein 50 Tage Durchschnitt verwendet werden. Steigt der kurzfristige 20 Tage Durchschnitt über den langfristigen 50 Tage Durchschnitt, entsteht ein Kaufsignal. Fällt der kurzfristige Durchschnitt unter den langfristigen Durchschnitt, erhalten wir ein Verkaufssignal.
Andere Crossover Strategien verwenden mehr als zwei Durchschnitte. In diesem Fall müssen die Durchschnitte in der Richtigen Reihenfolge übereinanderliegen.
Im Vergleich zu anderen gleitenden Durchschnitten kreuzen sich die Durchschnittslinien beim TEMA deutlich früher. Dadurch werden Signale zum Ein- und Ausstieg deutlich früher generiert. Das bedeutet aber nicht zwingend, dass die Trading Signale dadurch besser werden.
Fazit
Das ursprüngliche Ziel des Erfinders des TEMAs, einen Durchschnitt zu entwickeln, der mit deutlich weniger Verzögerung auf Trendänderungen reagiert, konnte also erreicht werden.
Diese schnelle Reaktionszeit hat allerdings sowohl Vor- als auch Nachteile. Bei relativ kurzfristigen Bewegungen kann schneller in eine Position ein- und wieder ausgestiegen werden. In diesen Fällen kann oft eine Position mit Gewinn geschlossen werden, während dieselbe Position bei anderen Durchschnitten erst später mit einem Verlust geschlossen worden wäre. Gleichzeitig sorgen die schnellen Ein- und Ausstiege allerdings auch dafür, dass in Trendphasen Positionen oft zu früh geschlossen werden und damit Teile der Bewegung verpasst werden.
Weitere Artikel
Liste der bekanntesten gleitenden Durchschnitte
Moving Average Crossovers | Strategien mit gleitenden Durchschnitten
Übersicht | Trendfolge Strategien