Der Double Exponential Moving Average (DEMA) ist ein gleitender Durchschnitt, der aus zwei exponentiellen gleitenden Durchschnitten (EMA) gebildet wird. Im Vergleich zu anderen gleitenden Durchschnitten reagiert der DEMA mit deutlich weniger Verzögerungen auf Kursänderungen.
Inhalt
Was ist der Double Exponential Moving Average?
Formel für Double Exponential Moving Average
Berechnung des DEMA
Der DEMA im Vergleich zu anderen Durchschnitten
Einsatz des DEMA im Trading
Was ist der Double Exponential Moving Average?
Der Double Exponential Moving Average wurde von Patrick Mulloy entwickelt. Mulloy störte sich daran, das gleitende Durchschnitte immer erst mit einiger Verzögerung auf Kursbewegungen reagieren. Mit dem DEMA versuchte er daher einen gleitenden Durchschnitt zu kreieren, der Kursbewegungen schneller abbildet und dadurch Trendwechsel früher anzeigt als herkömmliche Durchschnitte.
Wie alle gleitenden Durchschnitte wird der Double Exponential Moving Average meistens als Linie in den Kurschart eingetragen.
Dazu wird in einem Tageschart für jeden Tag der DEMA berechnet. Die Werte werden dann oberhalb der zugehörigen Tage in den Chart eingetragen und durch eine Linie verbunden.
Der Chart zeigt den Kursverlauf einer Aktie. Die rote Linie markiert den Verlauf eines Double Exponential Moving Average.
Formel für Double Exponential Moving Average
Um den DEMA zu berechnen, verwendete Mulloy einen „normalen“ exponentiellen gleitenden Durchschnitt (EMA) und einen geglätteten EMA, der aus den Werten des normalen EMA berechnet wurde.
Die Werte der beiden Durchschnitte werden in die untenstehende Formel eingetragen.
DEMAt = 2* EMAt – EMA(EMAt)
mit
EMAt = exponentieller gleitender Durchschnitt
EMA(EMAt) = exponentieller Durchschnitt des EMAt
Berechnung des DEMA
Die Berechnung der DEMA erfolgt also in drei Schritten:
- Im ersten Schritt wird der normale exponentiell gleitende Durchschnitt berechnet.
- Danach wird aus den Werten des EMA der geglättete EMA berechnet.
- Zuletzt werden die Werte der beiden EMA in die Formel von oben eingetragen.
Schritt 1. Berechnung des EMA
Zur Berechnung des exponentiell gleitenden Durchschnitts werden der Schlusskurs und der Kurs des vorherigen EMA benötigt. Die Werte werden dann in die unten stehende Formel eingesetzt.
EMAt = Ct * SF + (1-SF) *EMAt-1
und
SF = 2/ (n+1)
mit:
- EMAt = exponentiell gleitender Durchschnitt der betrachteten Periode (bspw. des heutigen Tages)
- EMAt-1 = exponentiell gleitender Durchschnitt der vorherigen Periode (bspw. des gestrigen Tages)
- Ct = Endkurs der betrachteten Periode (bspw. Schlusskurs des heutigen Tages)
- SF = Smoothing Factor
- n = Anzahl der Tage
Beispiel
Wir wollen den 10 Tage EMA für die Aktie A berechnen. Dazu berechnen wir zuerst den 10 Tage EMA der Aktie. Die Aktie ist bei einem Kurs von 110,60€ aus dem Handel gegangen. Der letzte Wert des EMA lag bei 108,43972. Wir setzen die beiden Werte nun in die Formel für den EMA ein.
Als Erstes berechnen wir den Smoothing Factor. Da wir den 10 Tage Durchschnitt berechnen möchten, setzen wir den Wert 10 für n ein.
SF = 2/ (10+1) = 0,1818
Nun können wir den Wert des SF in die Formel des EMA einsetzen.
EMA10 = 110,60€* 0,1818 + (1-0,1818) * 108,43972
EMA10 = 108,83250
Exkurs | Wo kommt der vorherige EMA her?
Beim Betrachten der Formel werden Sie sich vielleicht gefragt haben, wo der Wert für den vorherigen EMA herkommt. Da der EMA immer mit Hilfe des Wertes des vorherigen EMAs berechnet wird, muss es irgendwann einen Punkt geben, an dem der EMA auf eine andere Weise berechnet wurde.
Wie bereits zuvor erwähnt, muss der EMA immer für alle Tage im Chart berechnet werden, um die Durchschnittslinie einzeichnen zu können. Am ersten Tag der Berechnung wird dabei statt des nicht vorhandenen vorherigen EMAs einfach der Schlusskurs des Vortags eingetragen.
Schritt 2. Berechnung des geglätteten EMA
Im zweiten Schritt wird der geglättete EMA berechnet. Dazu wird aus dem Wert des EMA ein neuer EMA berechnet. Anstatt des Schlußkurses wird nun also der Wert des zuvor berechneten EMA in die Formel eingetragen. Als zweiter Wert wird der geglättete EMA des Vortags verwendet.
Beispiel
Wir fahren mit unserem Beispiel von oben fort. Wir nehmen an, dass der vorherige geglättete EMA einen Wert von 107,77704 hatte. Den Wert des EMA haben wir bereits in Schritt 1 berechnet.
EMA(EMAt) = EMAt * SF + (1-SF) * EMA(EMAt-1)
EMA(EMA10) = 108,83250*0,1818 * (1-0,1818)*107,77704
EMA(EMA10) = 107,96895
Schritt 3. Berechnung des DEMA
im letzten Schritt werden nun die zuvor berechneten Werte in die Formel des DEMA eingetragen.
DEMAt = 2* EMAt – EMA(EMAt)
DEMA10= 2* 108,83250 – 107,96895
DEMA10= 109,69606
Der DEMA im Vergleich zu anderen Durchschnitten
Als Nächstes wollen wir untersuchen, wie schnell der Double Exponential Moving Average im Vergleich zu anderen gleitenden Durchschnitten auf Kursänderungen reagiert. Wir vergleichen dabei den DEMA mit den zwei am meisten verwendeten gleitenden Durchschnitten, dem exponentiellen gleitenden Durchschnitt (EMA)und dem einfachen gleitenden Durchschnitt (SMA).
Um die Performance der drei gleitenden Durchschnitte vergleichen zu können, betrachten wir die fiktive Aktie A. Wir nehmen an, dass sich der Kurs der Aktie in den ersten 10 Tagen nicht bewegt und durchgängig bei hundert Euro notiert. Danach steigt der Kurs für 10 Tage um jeweils einen Euro, bis er 110€ erreicht. In den letzten 10 Tagen fällt der Kurs der Aktie jeden Tag um genau einen Euro. Der Kursverlauf der Aktie hat also ein pyramidenförmiges Aussehen.
Nun berechnen wir für diese Aktie den 10 Tage DEMA, den 10 Tage EMA und den 10 Tage SMA. Den Verlauf der drei Durchschnitte sehen Sie im untenstehenden Chart.
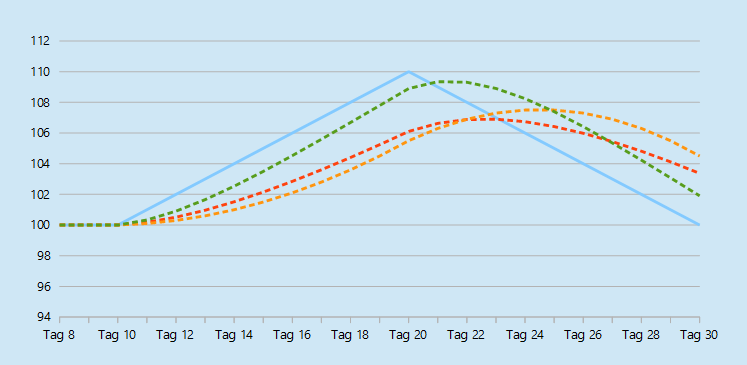
Da die ersten Tage nichts passiert, beginnt unser Chart erst ab Tag 8.
Der Kursverlauf der Aktie wird durch die blaue Linie dargestellt. Die grüne Linie zeigt den Verlauf des DEMA, die rote Linie zeigt den EMA und die orange den SMA.
Die Linie des Double Exponential Moving Average verläuft deutlich enger am Kurs als die Linien der anderen beiden Durchschnitte. Als die Aktie von einer Aufwärtsbewegung zu einer Abwärtsbewegung überging, reagierte der DEMA nur mit einer kurzen Verzögerung und drehte deutlich vor den anderen beiden Durchschnitten. Ebenso war der DEMA auch der erste Durchschnitt, der die Kurslinie nach dem Ende des Aufwärtstrends geschnitten hat.
Warum steigt und fällt der DEMA stärker als der EMA?
Um zu verstehen, warum der Double Exponential Moving Average so schnell auf Kursbewegungen reagiert, schauen wir uns noch einmal die Formel für den DEMA an.
DEMAt = 2* EMAt – EMA(EMAt)
Die Formel kann umgeschrieben werden in
DEMAt = EMAt + EMAt – EMA(EMAt)
Der Wert des DEMA setzt sich also zusammen aus dem Wert des EMA und der Differenz zwischen EMA und dem geglätteten EMA.
Um zu verstehen, was das für den Verlauf des Durchschnitts bedeutet, sehen wir uns den untenstehenden Chart an. Der Chart zeigt wieder den Kursverlauf der Aktie. Die grüne Linie und die rote Linie zeigen weiterhin den Verlauf des DEMA und des EMA an. Neu hinzu kommt die gelbe Linie, die den Verlauf des geglätteten EMA zeigt.
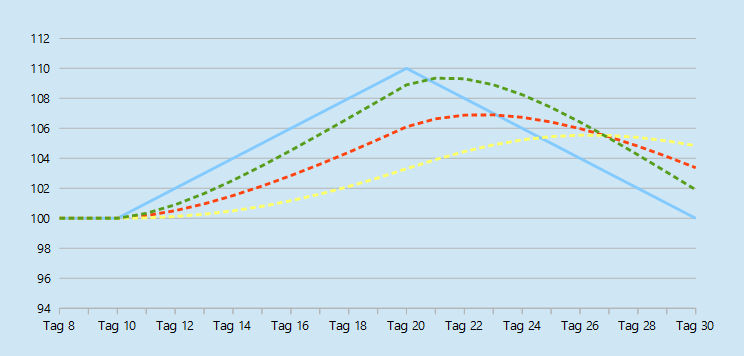
Der geglättete EMA reagiert weniger stark auf Kursbewegungen als der EMA. In einer Aufwärtsbewegung verläuft der geglättete EMA also unter dem normalen EMA. Je weiter die Kurse steigen, desto weiter bewegt sich die EMA vom geglätteten EMA weg.
Schauen wir uns noch einmal die Formel an.
DEMAt = EMAt + [ EMAt – EMA(EMAt)]
Wenn der Kurs über längere Zeit steigt, ist der geglättete EMA kleiner als der EMA. Der Wert in der eckigen Klammer ist also positiv. Dieser Wert wird nun zum EMA hinzugerechnet. Dies können Sie übrigens auch im Chart erkennen. Der Abstand zwischen EMA und geglättetem EMA entspricht immer genau dem Abstand zwischen EMA und DEMA.
- Der Wert des DEMA ist also bei steigenden Kursen immer größer als der Wert des EMA.
Anders sieht dies bei fallenden Kursen aus. Hier verläuft die Linie des EMA unter der Linie des geglätteten EMA. Der Wert in der Klammer ist also negativ und wird daher vom EMA abgezogen. Der Double Exponential Moving Average fällt nun also schneller als der EMA.
Einsatz des DEMA im Trading
Trendbestimmung
Der Double Exponential Moving Average kann, genau wie die meisten gleitenden Durchschnitte, zur Bestimmung des Trends genutzt werden. Dazu wird untersucht, ob sich der Kurs oberhalb oder unterhalb der Linie des gleitenden Durchschnitts befindet.
- Wenn die Kurslinie oberhalb des DEMA verläuft, so liegt ein Aufwärtstrend vor.
- Wenn die Kurslinie unterhalb des DEMA verläuft, liegt ein Abwärtstrend vor.
- Zu einem Trendwechsel kommt es, wenn die Linie des DEMA die Kurslinie kreuzt.
Da der DEMA deutlich enger am Kurs verläuft, kreuzt der Kurs die Linie des DEMA deutlich früher als die Linien anderer Durchschnitte. Trendwechsel werden im DEMA also deutlich eher angezeigt als bei anderen gleitenden Durchschnitten. Allerdings kann es dadurch auch zu einer etwas größeren Zahl von Fehlsignalen kommen.
Gerade beim DEMA lohnt es sich auch, auf den Verlauf der Durchschnittslinie zu achten. Eine steigende Linie zeigt einen Aufwärtstrend an. Eine fallende Linie zeigt einen Abwärtstrend an. Dreht die Linie deutet dies auf einen Trendwechsel hin.
Erzeugen von Trading Signalen
Der DEMA kann auch zum Erzeugen von Trading Signalen genutzt werden. Hierzu gibt es verschiedene Strategien, die alle als Moving Average Crossover Strategien bekannt sind.
- Bei der ersten Strategie wird eine Trading Position immer dann geschlossen, wenn der Kurs die Linie des Durchschnitts kreuzt. Steigt der Kurs einer Aktie über die Linie des DEMA, wird die Aktie gekauft. Fällt der Kurs unter die Linie wird die Aktie wieder verkauft.
- Die Double Crossover Methode nutzt zwei gleitenden Durchschnitte. Wenn sich die beiden Durchschnitte kreuzen, so wird ein Handelssignal generiert. Werden beispielsweise ein 10 Tage Durchschnitt und ein 20 Tage Durchschnitt verwendet, so entsteht ein Kaufsignal, wenn der 10 Tage Durchschnitt über der 20 Tage Durchschnitt steigt. Ein Verkaufssignal wird erzeugt, wenn der 10 Tage Durchschnitt unter den längeren Durchschnitt fällt.
- Die Triple Crossover Methode nutzt drei gleitende Durchschnitte. Hier entstehen Kauf- und Verkaufssignale, wenn die drei Durchschnitte in der richtigen Reihenfolge übereinanderliegen .
Der DEMA liefert in den meisten Fällen Ein- und Ausstiegssignale, bevor andere gleitende Durchschnitte wie etwa der EMA oder der SMA Handelssignale erzeugen.
Das ist Fluch und Segen zugleich. In kurzfristigen Seitwärtsbewegungen steigt der DEMA schneller in einen Trade ein und wieder aus. Dadurch steigt er oft mit einem Gewinn aus, während der langsamere EMA mit einem Verlust abschließt. In Trendphase steigt der DEMA aber auch häufiger bei einer kurzfristigen Gegenbewegung wieder aus dem Trade aus und verpasst so Teile des folgenden Anstiegs.
Ähnliche gleitende Durchschnitte
Ebenfalls von Patrick Mulloy entwickelt wurde der Triple Exponential Moving Average (TEMA), der noch ein wenig schneller auf Kursänderungen reagiert. Nach einem ähnlichen Berechnungsprinzip funktioniert auch der Hull Moving Average, der allerdings statt exponentiell gleitender Durchschnitte zwei verschiedene gewichtete gleitende Durchschnitte verwendet.
Weitere Artikel
Liste | Die wichtigsten gleitende Durchschnitte
Strategien mit gleitenden Durchschnitten